 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
I Направление выпуклости (вогнутости)
Пусть функция  дифференцируема на интервале
дифференцируема на интервале  . Дифференцируемость означает существование конечной производной, что, в свою очередь, означает наличие у графика функции невертикальной касательной. А для такой прямой есть понятия «выше» и «ниже».
. Дифференцируемость означает существование конечной производной, что, в свою очередь, означает наличие у графика функции невертикальной касательной. А для такой прямой есть понятия «выше» и «ниже».
Определение 1. Дифференцируемая функция  называется выпуклой вниз (вверх) на интервале
называется выпуклой вниз (вверх) на интервале  , если её график лежит не ниже (не выше) любой касательной к графику функции на
, если её график лежит не ниже (не выше) любой касательной к графику функции на  .
.
Говорят ещё: «график функции направлен выпуклостью вниз (вверх)». Вместо «выпукла вниз (вверх)» говорят иногда «вогнута вверх (вниз)». Ещё вместо «выпуклая вверх» говорят просто «выпуклая», а вместо «выпуклая вниз» – «вогнутая».
На рисунке слева изображен график функции выпуклой вниз, а справа – вверх.

Теорема 1 (первое достаточное условие выпуклости). Пусть функция 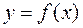 имеет на интервале
имеет на интервале  конечную производную второго порядка. Тогда:
конечную производную второго порядка. Тогда:
1) если 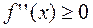 на
на  , то
, то  направлена выпуклостью вниз;
направлена выпуклостью вниз;
2) если  на
на  , то
, то  направлена выпуклостью вверх.
направлена выпуклостью вверх.
Доказательство. Обозначим:  – ордината точки графика функции с абсциссой
– ордината точки графика функции с абсциссой  ;
;  – ордината точки касательной к графику с той же абсциссой. Если
– ордината точки касательной к графику с той же абсциссой. Если  – произвольная точка из
– произвольная точка из  , то уравнение касательной к графику
, то уравнение касательной к графику  в точке с абсциссой
в точке с абсциссой 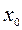 имеет вид:
имеет вид:  . Составим разность ординат:
. Составим разность ординат:  . Существование
. Существование  означает, что существует (и непрерывна)
означает, что существует (и непрерывна)  и, следовательно,
и, следовательно,  – непрерывна. Тогда к функции
– непрерывна. Тогда к функции  на промежутке
на промежутке  применима теорема Лагранжа:
применима теорема Лагранжа:

Тогда

Функция  непрерывная и дифференцируемая, значит, к ней можем приме-нить теорему Лагранжа на промежутке
непрерывная и дифференцируемая, значит, к ней можем приме-нить теорему Лагранжа на промежутке 

Итак, для разности ординат точки графика и точки касательной имеем равенство:  . Возможны два случая взаимного расположения точек
. Возможны два случая взаимного расположения точек  :
:

В обоих случаях произведение  положительно, следовательно,
положительно, следовательно,  : если
: если 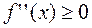 , то
, то  , т.е. график расположен выше касательной, функция выпукла вниз; если
, т.е. график расположен выше касательной, функция выпукла вниз; если  , то
, то  , график расположен ниже касательной, функция выпукла вверх. Теорема доказана.
, график расположен ниже касательной, функция выпукла вверх. Теорема доказана.
Замечание 1. Доказанная теорема имеет простую геометрическую иллюстрацию. Если функция выпукла вниз, то угловой коэффициент касательной, т.е.  возрастает, значит
возрастает, значит  . Для выпуклой вверх функции первая производная убывает, значит, вторая производная отрицательна.
. Для выпуклой вверх функции первая производная убывает, значит, вторая производная отрицательна.
Пример 1. Исследовать на выпуклость степенную функцию 
Имеем  . Если
. Если  или
или  , то
, то  , а если
, а если  , то
, то 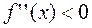 . Значит,
. Значит,  на луче
на луче  выпукла вниз при
выпукла вниз при  и
и  , и выпукла вверх при
, и выпукла вверх при  . При
. При  или
или  имеем линейную функцию
имеем линейную функцию 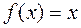 или
или  . Такие функции могут считаться как выпуклыми вверх, так и выпуклыми вниз.
. Такие функции могут считаться как выпуклыми вверх, так и выпуклыми вниз.
Поиск по сайту: