 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Примеры. 7. Найдём асимптоты графика функции
7. Найдём асимптоты графика функции  .
.
 – асимптота при
– асимптота при 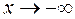 ,
,
 нет горизонтальной асимптоты при
нет горизонтальной асимптоты при 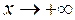 , но может быть наклонная:
, но может быть наклонная:


Итак, прямая  – наклонная асимптота графика функции
– наклонная асимптота графика функции  при
при 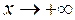 .
.
Заметим, что вертикальных асимптот график не имеет, ибо данная функция является непрерывной (в силу элементарности) на всей числовой оси.
8. Найти асимптоты графика функции  Очевидно, что гори-зонтальных асимптот нет, ибо
Очевидно, что гори-зонтальных асимптот нет, ибо  Далее,
Далее,


 .
.
Прямая  – наклонная асимптота графика функции
– наклонная асимптота графика функции  при
при 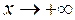 и при
и при 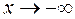 .
.
Замечание 2. Нетрудно заметить, что, если 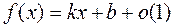 при
при 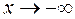 (
(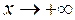 ), то прямая
), то прямая 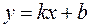 – наклонная асимптота графика функции при
– наклонная асимптота графика функции при 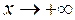 (
(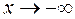 ).
).
Поиск по сайту: