 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Условие постоянства функции
Теорема. Если функция 
непрерывна на промежутке 
и во всех внутренних точках отрезка 
, то 
постоянна на этом промежутке.
Доказательство. Пусть 
. Применим теорему Лагранжа к функции 
на промежутке 
: 
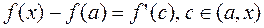. Но по условию 
, следовательно, 
и поэтому 
(на правом конце 
в силу непрерывности).
Пример. Рассмотрим функцию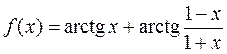 
на промежутке 
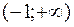. Её производная: 
Следовательно, 
const на 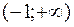. Чтобы найти эту константу, достаточ-но вычислить в любой точке, например, 
. Итак, мы доказали тождество 
.
В интегральном исчислении важное приложение найдет следствие, вытекающее из доказанной теоремы.
Следствие. Если функции и 
непрерывны на промежутке и имеют равные производные во всех внутренних точках промежутка, то эти функции всюду в отличаются лишь на постоянную: 
.
Для доказательства достаточно применить теорему к вспомогательной функции 
. Тогда 
и .
§2. Условие монотонности функции
Известно, что функция называется строго возрастающей на 
, если для любых точек 
из неравенства 
следует неравенство 
. Другими словами знак приращения функции совпадает со знаком приращения аргумента: 
. Для убывающей функции, естественно, 
.
Теорема. (Достаточное условие монотонности). Пусть функция дифференцируема на . Тогда:
1) если 
на , то 
строго возрастает на ;
2) если 
на , то строго убывает на .
Доказательство. Возьмём две произвольные точки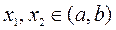 
, причём пусть . Применим теорему Лагранжа к функции на промежутке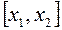 
(условия теоремы выполнены, ибо непрерывность вытекает из её дифференцируемости): 
По предположению 
, следовательно, знак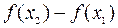 
определяется знаком производной. 1) Если , то и 
и 
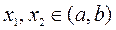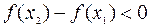; т.к. это верно для любых , то возрастает на . 2) Если , то и 
и 
, что означает убывание .
Замечание. Связь между знаком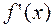 
и направлением изменения геометрически очевидна, если вспомнить, что производная – это угловой коэффициент касательной к графику . Однако, даже у строго монотонной функции касательная может быть и горизонтальной, т.е. 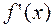для отдельных значений 
может обращаться в 0. Примером служит функция 
: она строго возрастает, но производная 
при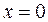 
обращается в ноль.
Итак, теорема сводит вопрос о возрастании (убывании) функции к решению неравенства ().
Пример. Исследовать на монотонность функцию 
. Находим производную и разлагаем её на множители: 
. Метод интервалов позволяет определить знак :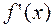
- 
На интервалах 
и 
функция возрастает, а на 
– убывает.
Поиск по сайту: