Формула Тейлора для многочлена. Бином Ньютона

Напомним формулу для вычисления производных (любого порядка) степенной функции с натуральным показателем степени:

С помощью этой формулы установим связь между коэффициентами многочлена п ^ой степени

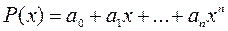(1)

и производными самого многочлена в нуле. Запишем многочлен в виде

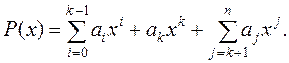
Первое слагаемое правой части после k –кратного дифференцирования обратится в ноль, а второе – в 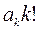. Для третьего слагаемого имеем:

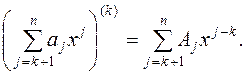
В этой сумме все показатели степени . Чтобы эта сумма обратилась в ноль, достаточно положить 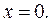Итак, получим связь:

Отсюда вытекает формула, выражающая коэффициенты многочлена через производные самого многочлена:

(2)

Теперь многочлен (1) можно записать в форме

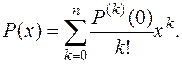
Напомним, что производная нулевого порядка – это сама функция.

Иногда требуется многочлен (1) записать не по степеням , а по степеням двучлена 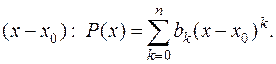Нетрудно убедиться, что в этом случае коэффициенты вычисляются по формуле 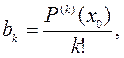а сам многочлен можно записать в виде

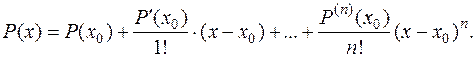
Это и есть формула Тейлора для многочлена.

Из формулы (2) для коэффициентов многочлена (1) можно вывести два важных следствия.

Следствие 1. Рассмотрим два многочлена

и

Есл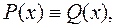и то и 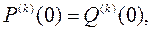откуда получим: а) степени многочленов равные – 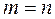; б) коэффициенты при одинаковых степенях переменной равные –

Следствие 2. Рассмотрим многочлен, представляющий собой 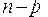степень бинома 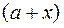и запишем его в стандартной форме (1):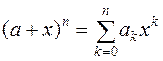

Коэффициенты вычислим по формуле (2):

Итак, мы получили т.н. формулу бинома Ньютона:

Числа обозначают и называют биномиальными коэффициентами. Так как 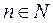, можно использовать компактную запись этих чисел:

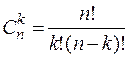
Это число возникают в задачах комбинаторики, где они называются «числом сочетаний из 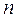по 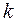» и дают ответ на вопрос: «Сколькими способами можно выбрать 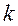предметов из 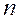предметов, если не важен порядок выбора?»

Пример. Запишем многочлен 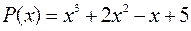по степеням 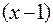. В соответствии с формулой Тейлора имеем:

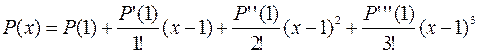
Здесь: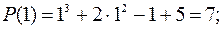

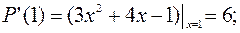
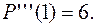
Итак,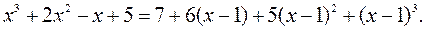

Поиск по сайту: