АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Биноминальное распределение

Читайте также:
  1. A) эффективное распределение ресурсов
  2. FRSPSPEC (Ф. Распределение средств.Статьи)
  3. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  4. II. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
  5. III. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
  6. III. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
  7. III. Распределение часов по темам и видам обучения
  8. III. Распределение часов по темам и видам обучения
  9. IV.2 Распределение часов по темам и видам учебной работы.
  10. UMENUTCP (ПП. Меню-требования - распределение продуктов по катег. дов.)
  11. UPRESTM (ПП. Распределение по времени приема пищи)
  12. Анализ факторов, влияющих на распределение доходов населения

Пусть производится n независимых испытаний, в каждом из которых соб.А может появиться либо не появляться. Вероятность наступления.

В мешке 4 белых и 2 черных шара. Одновременно берут 3 шара. Построить таблицу распределения вероятности числа белых шаров в выборке и график функции распределения.

Х= 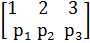р1 = р2= р3=

 

f(x)
 

 


>

х
1 2 3

 

Основные числовые характеристики любой случайной величины

Х является математическое ожидание mx=M[x] и дисперсия D[x] = M[(x-mx)]. Для дискретной случайной величины

Х=

mx=M[x] =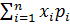

D[x] = M[(x-mx)2] =

Неотрицательное число называется среднеквадратичным отклонением случайной величины.

Физическая аналогия: если вероятности рассматривать как массы, сосредоточенные в точках х1 х2 … хn, то mx= M[x] является центром, а δх2= D[x] – момент инерции масс относительно центра. Дисперсия является характеристикой рассеяния случайной величины относительно центра. Чем меньше D, тем меньше рассеяние, тем «менее случайной» является величина х.

Основные свойства математического ожидания и дисперсии.

1) Если С – неслучайная величина (постоянная), то М(С) = С, М(СХ) = СМ(Х), D(C) = 0, D(СХ) = С2D(x)

2) M(X - для любых случайных величин.

D (X - для независимых X и Y.

X и Y – независимые, если распределительная вероятность каждой из них не зависит от того, какие значения приняли остальные величины.

3) При ɛ>0 выполняется неравенство Чебышева

Р(|x-mx| <ɛ)> 1-

Найти mx и D числа очков, выпавших при одном бросании игральной кости

Х =

mx=M[x] =

δx2=D[x]=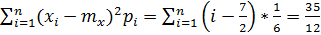

 

Вероятность попадания в цель при стрельбе из орудия р=0,6. Найти математическое ожидание общего числа попаданий, если произведено 10 выстрелов.

М(х)= n*p= 10*0,6=6 независимые события.

 

Событие во всех испытаниях постоянно и равно p (следовательно, вероятность непоявления q=1-p). Рассмотрим в качестве дискретной случайной величины х число появлений соб.А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины х. для ее решения требуется определить возможные значения Х и их вероятности. Очевидно, соб.А в n испытаниях может либо не появиться, либо появиться 1 раз, 2 раза, либо n раз.

Возможные значения х: 1,2,…n

Вероятности возможных значений вычисляются по формуле Бернулли:

Рn(k)= Сnkpkqn-k, где k= 0,1,2,…n – аналитическое выражение закона распределения.

Биноминальным называют распределение вероятностей, определяемое формулой Бернулли. Закон так назван, т.к. правая часть формулы – общий член разложения бинома Ньютона:

(p+q)n= Сnnpn + Cnn-1pn-1q+…+Cnkpkqn-k+…+Cn0qn

Таким образом, первый член разложения pn определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях, второй npn-1q – вероятность наступления события n-1 раз …, последний qn -, что событие не появится ни разу.

Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины х – числа выпадений «герба».

р=1/2, q=1-2

х1=2, х2=1, х3=0.

р2(2) =

р2(1) = С21 pq = 2*1/2*1/2=0,5

р2(0)= С20р2=(1/2)2=0,25

 

X      
P 0.25 0.5 0.25

Чаще всего в качестве случайной величины, распределенной по биноминальному закону рассматривается частота появления случайной величины А в n независимых опытах:

К =

Относительная частота k/n распределена также по биноминальному закону. Величины k и k/n имеют следующие числовые характеристики:

M[k] = np D[k] = npq

M[k/n] = p D[k/n] = pq/n

При n ⇾∞ D [k/n] ⇾0. Отсюда следует закон больших чисел Бернулли: при достаточно большом числе опытов относительная частота k/n является величиной почти неслучайной, она лишь незначительно колеблется около своего центра.

k/n ≈p n⇾∞

это вытекает из неравенства Чебышева.

Р()⇾1 при n⇾∞, т.е. неравенство практически достоверно при достаточно большом n.

 

Батарея производит залп из 6 орудий по цели. Вероятность попадания в цель для каждого орудия р=1/3. Построить распределение вероятности числа попаданий в цель (величина k). Определить вероятность того, что число попаданий будет от 1 до 3.

k=0,1,2,…..6 n=6 p=1/3 q =2/3

k=

pk=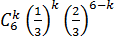

k=

наиболее вероятное число попаданий k=2

Вероятность того, что будет от 1 до 3 попаданий

Р(1≤k≤3) = p1+p2+p3=0,813


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)