АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Случайная величина. Законы распределения. Числовые характеристики случайных величин

Читайте также:
  1. Cущностные характеристики техники
  2. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  3. I. Схема характеристики.
  4. V2: Законы постоянного тока
  5. V2: Законы сохранения в механике
  6. А выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид
  7. А) федеральные законы и нормативные акты
  8. А) федеральные законы и нормативные документы
  9. А. Простая, единичная, или случайная, форма стоимости
  10. А. Средняя квадратическая погрешность функции измеренных величин.
  11. Акустические колебания, их классификация, характеристики, вредное влияние на организм человека, нормирование.
  12. Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение. Случайная величина является числовой характеристикой исхода опыта и относится к основным понятиям теории вероятностей, принято обозначать заглавными буквами X,Y,…….; принимаемые ими значения – строчными x,y…..

Дискретной случайной величиной называется случайная величина, принимающая отделенные друг от друга значения, которые можно пронумеровать, т.е. они образуют последовательность {x1, x2,….xn}.

Непрерывная случайная величина – с.в., возможные значения которой непрерывно заполняют какой-либо промежуток.

Закономерное распределение с.в. – всякое соотношение, устанавливающее связь между возможными значениями с.в. и соответствующими им вероятностями. Закономерное распределение может иметь различные формы.

Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные значения этой с.в. с соответствующими им вероятностями. Эта таблица и выражает закон распределения.

 

Х х1 х2
р р1 р2

рi


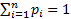
х1 х2 х3 х4

 

хi

Если последовательность {x1, x2,….xn} бесконечная, то ряд сходится и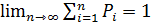

Графическое изображение ряда – многоугольник распред.

Функция распред. с.в. Х – F(x), выражающая вероятность того, что Х примет значение, меньшее х.

F(x) = P(X<x); F(x) – неубывающая функция.

F(-∞) = 0; F(+∞) = 1; Р(а<X<b)=F(b) – F(a).

Для с.в. дискретной:

F(x)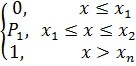

График F(х) – ступенчатая неубывающая функция, имеющая скачки в точках х1

С.в. Х называют непрерывной, если существует такая неотрицательная, интегрируемая в бесконечном промежутке функция f(x), называемая плотностью распределения вероятности.

F(x) = P(X<x) = F(x) = f᾿(x), P(a<X<b) =

 

Детали попадают к двум контролерам. Вероятность того, что деталь попадет к первому контролеру = 0,6; ко второму = 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером 0,94, а вторым 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

Н1 – дет. проверил первый контролер.

Н2 – дет. проверил второй контролер.

РА(Н1) =

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)