АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Сочетания с повторениями

Читайте также:
  1. Вводные слова и словосочетания
  2. Вводные слова и словосочетания в алфавитном порядке
  3. Вводные слова, словосочетания, вставные конструкции. обращения
  4. Влияние на организм неправильного сочетания пищевых веществ
  5. Гласные звуки и звукосочетания
  6. Задание 10 вводные слова, словосочетания, вставные конструкции. обращения
  7. Значение сочетания болезней сердца и сосудов с беременностью
  8. Оценка сочетания различных факторов, повлиявших на негативный исход
  9. Предложные терминологические словосочетания
  10. Размещения с повторениями.
  11. Синтаксическая связь слов в словосочетаниях
  12. Составьте словосочетания с данными паронимами так, чтобы показать разницу в значениях

а1 а2 аааааааа
Имеется k одинаковых экземпляров множества M, состоящего из n различных элементов. Из каждого экземпляра выбирается по одному элементу, и все элементы смешиваются. Получается неупорядоченная выборка {a1, a2,…ak}, в которой элементы могут повторяться. Число таких выборок равно – число сочетаний из n элементов по k с повторениями.

· Кость домино - сочетание из 7 цифр.

М={0,1,2,3,4,5,6} по 2 с повторениями.

Число таких выборок

Частная производная k-го порядка от функции u (x1, x2,…xn) n переменых

n1,n2,…nk – номера переменных, по которым происходит дифференцирование. Номера могут повторяться, их порядок несущественен

{n1n2…nk} – сочетание с повторением из n элементов по k. Число таких выборок – число частных производных.

Число частных производных второго порядка от функции трех переменных

 

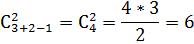
Случайное событие может либо произойти, либо нет в результате выполнения некоторых совокупностей условий.

Событие – результат испытания.

События несовместные, если появление одного из них исключает появление другого в одном и том же испытании.

Из ящика с деталями извлечена одна деталь. Появление стандартной детали исключает появление нестандартной.
Брошена монета. Появление герба исключает решку.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате появится одно и только одно из этих событий.

Стрелок выстрелил по цели. Обязательно произойдет одно из двух событий: промах, попадание. Эти два несовместимых события образуют полную группу.

События равновозможные, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Появление герба и решки – равновозможное событие.
Появление того или иного числа очков на брошенной игральной кости – равновозможное событие.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)