АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Неравенство Чебышева. Справедливо для дискретных и непрерывных случайных величин

Читайте также:
  1. А) Безграничное конкретное множество; b) равенство (неравенство).
  2. Билет 22Понятие евклидова пространства, неравенство Коши-Буняковского. Теорема Кронекера Капелли.
  3. Вопрос 22. Экономическое неравенство. Кривая Лоренца. Государственная политика социальной защиты населения в Украине
  4. Второе начало термодинамики. Самопроизвольные и несамопроизвольные процессы. Равенство и неравенство Клаузиуса.
  5. Доходы населения, источники их формирования (трудовые и нетрудовые, легальные и нелегальные) и распределение. Неравенство доходов и их причины
  6. Доходы населения: виды, источники. Неравенство доходов. Кривая Лоренца. Коэффициент Джини. Распределение и доходы.
  7. Имущественное неравенство в исторической перспективе
  8. Неравенство в доходах. Бедность и пути ее преодоления.
  9. НЕРАВЕНСТВО В РАСПРЕДЕЛЕНИИ НАЦИОНАЛЬНОГО ДОХОДА. КРИВАЯ ЛОРЕНЦА. КОЭФФИЦИЕНТ ДЖИННИ
  10. Неравенство доходов. Причины неравенства. Определение бедности, методы измерения неравенства доходов. Кривая Лоренца.
  11. Неравенство заработной платы после 1980-х
  12. Неравенство Коши-Буняковского.

Справедливо для дискретных и непрерывных случайных величин.

Пусть х – дискретная величина.

Р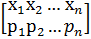

Надо оценить вероятность того, что отклонение случайной величины от её математической ожидаемости не превышает по абсолютной величине положительное число ɛ

Неравенство Чебышева: вероятность того, что отклонение случайной величины Х от её М(Х) по абсолютной величине меньше положительного числа ɛ, не меньше чем 1-D(x) /ɛ2

P(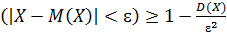

Событие, состоящее в осуществлении неравенства

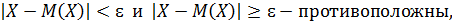
Сумма их вероятностей равна 1, тогда

(1)

D(X) = [X1-M(X)]2p1+ [X2-M(X)]2p2+… [Xn – M (X)]2pn

Все слагаемые неотрицательны.

Отбросим те слагаемые, у которых 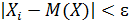(для оставшихся сумма от этого только уменьшится. Пусть отброшено k первых слагаемых

D(X)≥[Xk+1 – M(X)]2pk+1 + [Xk+2 – M(X)]2pk+2 +…+[Xn – M(X)]2pn

Обе части неравенства 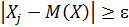положительные, тогда

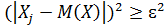, усилим неравенство D(X) ≥ɛ2(pk+1+pk+2+…+pn)

По теореме сложения вероятность pk+1+pk+2+…+pn есть вероятность того, что с.в. Х примет одно, безразлично какое, из значений Хk+1, Хk+2…Xn, а при любом из них отклонение удовлетворяет неравенству .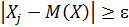

Отсюда следует, что сумма pk+1+pk+2+…+pn выражает неравенство

P(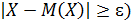

D(X) ≥ɛ2P )

P(

P(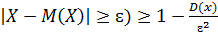

Неравенство Чебышева дает грубую оценку.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)