АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Распределение Пуассона

Читайте также:
  1. A) эффективное распределение ресурсов
  2. FRSPSPEC (Ф. Распределение средств.Статьи)
  3. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  4. II. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
  5. III. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
  6. III. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
  7. III. Распределение часов по темам и видам обучения
  8. III. Распределение часов по темам и видам обучения
  9. IV.2 Распределение часов по темам и видам учебной работы.
  10. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  11. UMENUTCP (ПП. Меню-требования - распределение продуктов по катег. дов.)
  12. UPRESTM (ПП. Распределение по времени приема пищи)

Если число испытаний n велико, то для определения вероятности k появлений события в этих испытаниях используют формулу Лапласа. Однако, эта ф-ла непригодна, если вероятность события мала (р≤0,1). В этих случаях (n велико, р мало) прибегают к асимптотической ф-ле Пуассона.

Сделаем важное допущение np – сохраняет постоянное значение, np = λ – это означает, что среднее число появлений событий в различных сериях испытаний, т.е. при различных значениях n, останется неизменным.

Воспользуемся ф-лой Бернулли:

pn(k) =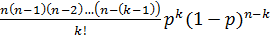

np=λ, p=

pn(k)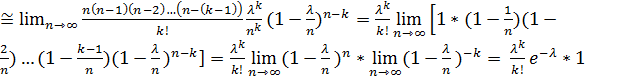

 

pn(k)=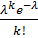

Завод отправил на базу 500 изделий. Вероятность повреждения изделий k штук равна 0,002. Найти вероятность того, что в пути будет повреждено изделий: а) ровно 3; б) менее 3; в) более 3; г) хотя бы одно.

λ=n*p=500*0.002=1

а) р500(3) = 13 е-1/3! = 0,0613

б) р(х<3)= р500(0) +р500(1) + р500(2) = е-1+ е-1+ е-1 /2 = 0,9197

в) а=1-р(х≤3) = 1- [p500(0) + p500(1) + p500(2) + p500(3)] = 0,019

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)