АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Сочетание без повторений

Читайте также:
  1. БОЖЕСТВЕННОЕ БРАКОСОЧЕТАНИЕ
  2. Для описания множественного типа используется словосочетание set of (множество из...).
  3. Какое сочетание фармакологических средств является адекватным при лечении отека легких на фоне высокой артериальной гипертензии больного с острым инфарктом миокарда?
  4. Классы путей, как сочетание групп и категорий.
  5. Личностные качества предпринимателя: нацеленность на результат, изобретательность, воля к действию, сочетание ума и фантазии.
  6. Определить тип гармонии: сочетание трех и более хроматических цветов контрастная полихромная
  7. Отрицание от сатаны и сочетание Христу.
  8. Перестановки. Размещение без повторений.
  9. Подлежащее-словосочетание
  10. Применение и сочетание методов воспитания
  11. Размещение без повторений
  12. Роман М. Булгакова «Мастер и Маргарита». Сочетание конкретно-исторической и гротескно-фантастической образности.

Если из множества М одновременно берут k элементов, то получается выборка (а1, а2,… ак), в которой порядок элементов несущественен (неупорядоченная выборка). Её можно рассматривать как подмножество множества М. Число таких выборок Cnk = = . Это число сочетаний из n элементов по k без повторения. Точно так же определяется число n-значных последовательностей (а1 а2… аn) из двух элементов, например 0 и 1, один из которых повторяется k раз, другой n-k раз (перестановки с повторениями). При k>n\2 вычисление упрощается =

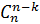
· Из колоды 36 карт одновременно берут 3 карты. Порядок карт в выборке {k1 k2 k3} несущественен.

А) чему равно число всевозможных троек карт?

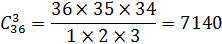
Б) сколько можно выбрать троек, содержащих одного туза?

·

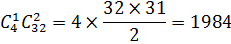
Г
ординатная плоскость покрыта квадратной сеткой со стороной квадрата 1. Чему равно число кратчайших путей, идущих по сетке из (0;0) в точку (m;n)?

В
В
Г
Г

Г
В
 

(ГВГГВВГ) – перестановка с повторением.
Число элементов = m+n. Г повторится m раз, В – n раз. Число таких перестановок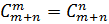

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)