АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формула полной вероятности

Читайте также:
  1. II Формула Тейлора с остаточным членом в форме Пеано
  2. III Формула Тейлора с остаточным членом в форме Лагранжа
  3. Анализ вероятности
  4. Банкротство и неплатежеспособность. Оценка вероятности банкротства.
  5. Барометрическая формула
  6. Барометрическая формула. Распределение Больцмана.
  7. Барометрическая формула. Распределение Больцмана.
  8. Барометрическая формула. Распределение Больцмана.
  9. Безусловные вероятности состояний марковской цепи
  10. Бесконечная струна. Метод распространяющихся волн. Формула Даламбера.
  11. Билет 12 Различные уравнения прямой на плоскости, геометрический смысл параметров. Формула преобразования координат вектора при переходе к новому базису
  12. Бюджетная и денежная политика в условиях полной мобильности капитала.

Пусть события Н1, Н2 … Нn (гипотеза) попарно несовместны и являются полной группой исходов данного опыта.

Для любого события А, являющегося результатом данного опыта, справедливы равенства

Р(А) = – формула полной вероятности

 

Доказательство: По условию соб.А может наступить, если наступит одно из несовместных событий Hi. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместн. Соб.Н1А, Н2А … НnА.

Теор. сложен. Р(А) = Р(Н1А) + Р(Н2А) + … Р(НnА)

По теор. умножения зависимое событие Р(Н1А)=Р(Н1) * РН1(А) и т.д.

Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная = 0,8, а второго = 0,9. Найти вероятность того, что взятая наудачу деталь стандартная.

А – извлеченная дет. стандартная.
вынута из 1 набора Р(Н1) = ½

вынута из 2 набора Р(Н2) = ½

условн. вер.

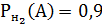
Р(А) = Р(Н1) * 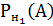+ Р(Н2) =0,5*0,8+0,5*0,9=0,85

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)