АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Дискретные случайные величины

Читайте также:
  1. A) Прямую зависимость величины предложения от уровня цены.
  2. I. Оценка изменения величины и структуры имущества предприятия в увязке с источниками финансирования.
  3. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  4. IV. Относительные величины, динамические ряды
  5. V. Вариационные ряды, средние величины, вариабельность признака
  6. Абсолютные величины
  7. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ
  8. Алгоритм изменения дозы НФГ в зависимости от относительной величины АЧТВ (по отношению к контрольной величине конкретной лаборатории)
  9. Аналоговые, дискретные и цифровые сигналы
  10. БАЗОВЫЕ ДОЗИМЕТРИЧЕСКИЕ ВЕЛИЧИНЫ
  11. Величины
  12. Величины спроса и предложения и цены на мороженое

Дискретной(прерывной) называют случайную величину, которая принимает отдельные изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Законом распределения дискретной случ.вел. называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка – возможные значения, вторая – их вероятности.

Х Х1 X2 X3 ……. Xn
Р P1 P2 P3 …….. Pn

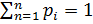
В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 рублей и десять выигрышей по 1 рублю. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца лотерейного билета.

Возможные значения Х: х1=50, х2=1, х3=0

р1=0,01 р2=0,1 р3=(1-р1-р2)=0,89

Х 50 1 0
р 0,01 0,1 0,89

 

Многоугольник распределения.

 

 

 

f(x)
График функции распределения F(x)

 
0 1 2 3

 

 


Наиболее общая характеристика любой случайности величина Х – функция распределения.

F(x) = P(X<x) – вероятность попадания случайной величины в интервал (-∞; х), где х – любое число.

Общие свойства F(x):

1)F(x) – неотрицательная функция

2)

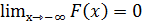
Для дискретной случайной величины функции распределения

F(x) – суммирование по всем допустимым значениям хi<х. При переходе через каждое допустимое значение хi F(х) меняется скачком на величину рi.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)