АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Размещение без повторений

Читайте также:
  1. III. Смешанное (квартирно-бивачное) размещение
  2. IV. размещение в оборонительных (фортификационных) сооружениях
  3. Альтернативный метод учета затрат на размещение
  4. Вопрос 11Трудовая миграция и проблемы с ней связанные. Влияние миграции на развитие и размещение производительных сил страны.
  5. Вопрос 21 Экологическая обстановка в регионах РФ, связанная с размещением производительных сил и нерациональной системой природопользования.
  6. Вопрос 39Топливная промышленность РФ: состав, размещение
  7. Вопрос 40Металлургический комплекс России: состав, современное состояние, размещение, металлургические базы, проблемы развития
  8. Вопрос 44Лесная, деревообрабатывающая и целлюлозно-бумажная промышленность: значение, состояние, размещение и проблемы развития
  9. Вопрос 46Структура сельскохозяйственного производства и его особенности. Факторы, влияющие на развитие и размещение
  10. Вопрос 48Размещение важнейших отраслей растениеводства и животноводства по территории страны
  11. Вопрос № 59. Инженерные подземные сети (ИПС) и их размещение на городских территориях.
  12. Выбор аппаратуры связи и ее размещение

Элементы комбинаторики

Имеется k множеств: М1, М2,… Мk с числом элементов n1, n2,… nk. В каждом множестве все элементы различны, а сами множества могут быть одинаковы.

Выберем по одному элементу из каждого множества a1 є M1, a2 є M2,… ak є Mk и образуем последовательность (а1, а2,… ак). Она называется упорядоченной выборкой. Число таких выборок равно произведению n1 × n2…nk. Точно так же определяется общее число способов, которыми можно выполнить k действий, если первое действие можно выполнить n1 способами, второе – n2 … nk способами.

· Сколько трехзначных целых чисел начинается и кончается четной цифрой?

Каждое такое число есть упорядоченная выборка (а1 а2 а3) из трех множеств а1 є {2,4,6,8}; а2 є {0,1,3 … 9}; a3 є {0,2,4,6,8}.

Число таких выборок n1n2n3 = 4×10×5 = 200

 

Размещение с повторениями

Имеется одно множество М из n элементов. Выберем из него последовательно по одному элементу и образуем выборку (а1, а2,…аk) из k элементов, причем берем элемент, записываем его и возвращаем обратно в множество М.

В полученной выборке каждый элемент может повториться. Число таких выборок определяется по правилу умножения n×n…n = nk.

· Чему равно число шестизначных телефонных номеров, если номер может быть любым набором шести десятичных цифр?

(а1 а2 а3 а4 а5 а6) – размещение с повторением из множества {0,1,2,…9}

Число таких размещений nk =106 = 1 000 000.

 

Размещение без повторений

Если выбранные из множества М элементы обратно не возвращают, то после k выборов получается упорядоченная выборка (а1 а2 …ак), в которой ни один элемент не повторяется, число таких выборок равно 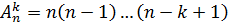– число размещений из n элементов по k без повторения.

При k=n =n!

Перестановки – выборки из генеральной совокупности из n элементов по n элементов в каждой.

· Сколько шестизначных номеров с неповторяющимися цифрами?

· Сколько шестизначных целых чисел можно составить из цифр 1,2,3,…6 (без повторяющихся цифр)

6!=720


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)