АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Классическое определение вероятности. Теория вероятности изучает модели опытов, результатом которых являются случайные события – исходы опытов

Читайте также:
  1. Access. Базы данных. Определение ключей и составление запросов.
  2. I. Дифракция Фраунгофера на одной щели и определение ширины щели.
  3. I. Определение
  4. I. Определение
  5. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  6. I. Определение пероксида водорода (перекиси водорода)
  7. I. Определение проблемы и целей исследования
  8. I. Определение ранга матрицы
  9. I. Пограничное состояние у новорожденных детей. Определение, характеристика, тактика медицинского работника.
  10. I. Сестринский процесс при гипертонической болезни: определение, этиология, клиника. Принципы лечения и уход за пациентами, профилактика.
  11. I. Сестринский процесс при диффузном токсическом зобе: определение, этиология, патогенез, клиника. Принципы лечения и ухода за пациентами
  12. I. Сестринский процесс при остром инфаркте миокарда: определение, клиника, неотложная помощь, транспортировка пациента.

Теория вероятности изучает модели опытов, результатом которых являются случайные события – исходы опытов. Предполагается, что любой исход опыта сводится к элементарным исходам. Множество всех элементов исходов Ω= {ω}. В результате опыта должен произойти один и только один элементарный исход ω в Ω. Любому событию А соответствует некоторое подмножество Ω в следующем смысле: соб. А наступает тогда и только тогда, когда произойдет какой-либо элементарный исход, принадлежащий соответствующему подмножеству. Событие и соответствующее ему подмножество обозначается одним символом. Событие, соответствующее всему множеству Ω, называется достоверным. Его вероятность принимается равной Р(Ω)=1.
Событие, соответствующее пустому множеству, невозможное.

Вероятностным событием А называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементов исходов, образующих полную группу.

P(A)= 0≤P(A)≤1

Частный случай, все исходы равновозможны. Число исходов n, сумма вероятности всех исходов = 1, вероятность каждого исхода . Событию А благоприятствует m исходов.

P(A)= - m слагаемых

P(A)=

(Урновая схема) В мешке 10 шаров, 6 белых и 4 красных. Определить вероятность события а) все 3 шара окажутся белыми; б) будет 2 белых и 1 красный.
Элементарный исход опыта - появление выборки 3 шаров из 10: ω= {ω­1, ω2, ω3} – сочетание без повторения. Они образуют множество всех элем. исходов опыта Ω={ 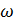}. Их число n =

Событию А соответствует выборка ω={51, 52, 53} – 3 белых шара. Число таких выборок N(A) =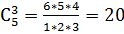

Событию B – ω{51,52,K3}

N(B)=

P(A) =20/120 P(B) =60/120

Какова вероятность того, что среди n лиц по крайней мере двое име6ют один и тот же день рождения в году (соб R)?

Пусть {d1 ,d2,…du} – дни рождения n лиц – выборка из множества 365 дней года – размещенные с повторениями.

N(Ω) =365­n

Найдем вероятность противоположного события 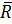, что n лиц имеют разные дни рождения – выборки с неповторяющимися элементами – размещение без повторения.

N( ) =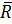

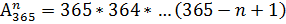
Р( ) =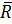

Искомая вероятность P(R) = 1-P( ) =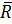

Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях – четная, причем на грани хотя бы одной из костей появится шестерка.

На выпавшей грани «первой» игральной кости может выпасть одно, два,… шесть очков. Аналогичные шесть элементарных исходов возможны при бросании «второй» кости. Каждый из исходов бросания «1» кости может сочетаться с каждым из исходов бросания «2» кости. Таким образом, общее число возможных элем. исходов 6*6=36 – полная группа и в силу симметрии костей – равнозначная.

Благоприятствующими интересующему нас событию(хотя бы на одной грани – «6», сумма выпавших очков – четная) являются следующие пять исходов:

1) 6;2 2) 6;4 3) 6;6 4) 4;6 5) 2;6

Искомая вероятность Р=5/36

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)