 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Противоположные события
Противоположными называют два единственных возможных, образующих полную группу (А и Ᾱ) (попадание и промах)
Теорема: Сумма вероятностей противоположных событий = 1. Р(А) + Р(Ᾱ) = 1.
Доказательство: Противоположные события образуют полную группу, следовательно сумма вер. их = 1.
Вероятность того, что день будет дождлив = 0,7, тогда вероятность ясной погоды = 0,3.
Произведением событий А и В называется новое событие А*В, которое наступает тогда, когда наступают оба события А и В одновременно.
Другими словами, подытожим:
| А |
| В |
| А |
| А |
| В |
Ᾱ А+В А*В
Два стрелка производят по одному выстрелу по цели. Пусть событие А1А2 – попадание в цель первого и второго стрелка. Тогда:
А1 + А2 – одно или два попадания (хотя бы одно)
А1*А2 – два попадания
А1* Ᾱ2 + Ᾱ1*А2 – одно попадание.
Ᾱ1+ Ᾱ2 = Ᾱ1 Ᾱ2 – ни одного попадания (два промаха)
Взаимно независимые события А1А2…Аn, если вероятность каждого из них не меняется от того, наступили или нет остальные события. Вероятность произведения взаимно независимых событий равна произведению вероятностей
Р(А1*А2*…*Аn) = Р(А1) * Р(А2) * … * Р(Аn).
Три стрелка одновременно выстрелили по мишени. Вероятности их попадания р1=0,8; р2 = 0,7; р3= 0,4 не зависят друг от друга. Определить вероятность того, что в мишени будут:
а) 3 пробоины; б) ни одной пробоины; в) по крайней мере одна; г) ровно одна
а) Р(А) = Р(А1А2А3) = Р(А1) * Р(А2) * Р(А3) = 0,8*0,7*0,4=0,224
б) Р(В) = Р(Ᾱ1)*Р(Ᾱ2)*Р(Ᾱ3) = 0,2*0,3*0,6= 0,036
в) Р(С) = Р(А1+А2+А3) =1 –Р(Ᾱ1+ Ᾱ2* Ᾱ3) = 1-0,036 = 0,964
г) Р(D) = Р(А1* Ᾱ2* Ᾱ3 + Ᾱ1 *А2* Ᾱ3 + Ᾱ1* Ᾱ2* А3) = =0.8*0.3*0.6+0.2*0.7*0.6+0.2*0.3*0.4 = 0.252
Условная вероятность
Вероятность события В при дополнительном условии, что произошло событие А.
РА(В) или Р(В/А)
В урне три белых и три черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (соб.В), если при первом испытании был извлечен белый шар (соб.А).
После первого испытания осталось 5 шаров, из них 3 белых. Искомая условность вероятности РА(В) = 3/5
Этот же результат можно получить по формуле
РА(В) = 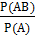 (Р(А)>0)
(Р(А)>0)
Теорема умножения произведения двух событий: Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
Р(АВ) = Р(А) *РА(В)
Доказательство из определения условной вероятности.
Следствие: Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условную вероятность всех остальных, причем вероятность каждого из последующего вычисляется в предположении, что все предыдущие уже появились.
Доказательство теоремы умножения для схемы случаев
Пусть возможные исходы опыта сводятся к n случаям, которые изобразим в виде n точек k~В
m~A Событие А благоприятствует m случ.
………………………………………………….. В k
l~AB
n Так как мы не предполагали А и В несовместными, то существуют случаи, благоприятные А и В одновременно. Число таких случаев – l. Тогда Р(АВ) = l/n. Р(А) = m/n
Вычислим Р(В/А) т.е. усл. вероятности случаев В при условии, что с А произошло. Если А произошло, то из ранее возможных n случаев остаются возможными только те m, которые благоприятствовали случаям А. Из них l случаев благоприятны случаям В, следовательно
Р(В/А) = l/m.
Р(АВ) = Р(А) * Р(В/А).
l/n = m/n * l/m – тождество.
Следствие 1: Если случай А не зависит от случая В, то и случай В не зависит от случая А.
Случай А не зависит от случая В, т.е. Р(А) =Р(А/В)
Требуется доказать Р(В) = Р(В/А)
Будем считать, что Р(А)≠0
Напишем теорию умножения в двух формах
Р(АВ) = Р(А) * Р(В/А)
Р(АВ) = Р(В) * Р(А/В)
Р(А)*Р(В/А) = Р(В)*Р(А) (по условию)
Р(В/А) = Р(В)
| 0,2 |
| 0,4 |
| 0,3 |
А→В-1
В→А-2
А→В-3
1) поражен. А 2) В
1) Для выполнения события – поражен. А необходимо совмещение (произведение) двух событий: А не поразил В, В поразил А.
Р(А) = 0,8*0,3=0,24
2) В =В1+В2, В1 – А поразил В (1 раз)
В2 – А поразил В (2 раза)
Р(В1)= 0,2
Р(В2) = 0,8*0,7*0,4=0,224
Р(В) = 0,2 + 0,224 = 0,424
В мешке 3 белых и 3 черных шара. Последовательно извлекаются по 2 шара без возвращения. Какова вероятность того, что шары каждой пары будут разного цвета?
Пусть Аi(i=1,2,3) означает, что шары i-ой пары разного цвета. События А1, А2, А3 зависимы
Р(А1А2А3) = Р(А1)*Р(А2)*Р(А3) = 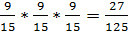
Поиск по сайту: