АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений

Читайте также:
  1. B. Советы по выполнению теста
  2. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  3. I.2.4. Алгоритм симплекс-метода.
  4. II. 4.1. Алгоритм метода ветвей и границ
  5. LU – алгоритм нахождения собственных значений для несимметричных задач
  6. QR- алгоритм нахождения собственных значений
  7. SALVATOR - это переход физического явления в семантико-нейронный алгоритм (инструкцию) освобождения человека от негативных последствий этого явления.
  8. V. Пакет контрольных заданий для текущей и промежуточной аттестации
  9. VI. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ТЕКУЩЕГО КОНТРОЛЯ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
  10. VI. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ТЕКУЩЕГО КОНТРОЛЯ УСПЕВАЕМОСТИ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
  11. X. примерный перечень вопросов к итоговой аттестации
  12. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ

Гипотеза(1):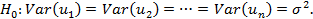

Шаг 1. Уравнения наблюдений объекта следует упорядочить по возрастанию суммы модулей значений предопределенных переменных модели (2),

т.е. по возрастанию значений

Шаг 2. По первым упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величину где - МНК-оценка случайного возмущения

Шаг 3. По последним упорядоченным уравнениям наблюдений вычислить МНК-оценки параметров модели и величину (аналогично).

Шаг 4. Вычислить статистику, для этого делим большее на меньшее, к примеру, если ESS1больше ESS2: .

Шаг 5. Задаться уровнем значимости и с помощью функции FРАСПОБР Excel при количествах степеней свободы , где определить (1- -квантиль, распределения Фишера.

Шаг 6. Принять гипотезу (1), если справедливы неравенства

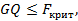
Т.е. при справедливых неравенствах случайный остаток в модели (2) полагать гомоскедастичными. В противном случае гипотезу (1) отклонить как противоречащую реальным данным и сделать вывод о гетероскедастичности случайного остатка в модели (2).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)