АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Интервальная оценка ожидаемого значения зависимой переменной в парной регрессионной модели

Читайте также:
  1. I. Оценка изменения величины и структуры имущества предприятия в увязке с источниками финансирования.
  2. I. ОЦЕНКА НАУЧНОГО УРОВНЯ ПРОЕКТА
  3. II РЕСЕНТИМЕНТ И МОРАЛЬНАЯ ОЦЕНКА
  4. II Универсальная оценка остаточного члена
  5. II. Структура и использование земель сельскохозяйственного назначения
  6. II.2. Задача о назначениях
  7. III. Используемые определения и обозначения
  8. III. Количественная оценка влияния показателей работы автомобиля на его часовую производительность
  9. III. Оценка давления и температуры воздуха в КС.
  10. Root(Выражение, имя переменной)
  11. V. ОЦЕНКА ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ
  12. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная

Эконометрические модели предназначены для объяснения (прогноза) текущих значений зависимой переменной по заданным (наблюдаемым) значениям предопределенных (независимых) переменных. Например, модель линейной парной регрессии создаетсядля прогноза значений зависимой (эндогенной) переменной y по заданным (наблюдаемым) значениям экзогенной переменной х (регрессора модели). Прогнозировать значения переменной можно лишь тогда, когда модель признана адекватной. Для проверки адекватности модели линейной парной регрессии рассчитываем нормированную ошибку прогноза по формуле , где – прогноз, 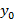- наблюдаемое в реальности значение переменной, - средняя квадратическая ошибка прогноза.

При этом если случайный остаток в рассматриваемой модели не имеет автокорреляции и нормально распределен, то tподчиняется закону распределения Стьюдента с числом степеней свободы , где k+1 – количество оцениваемых коэффициентов модели (для модели линейной парной регрессииk+1=2).Данное обстоятельство позволяет построить замкнутый интервал 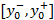с границами , именуемый доверительным интервалом, который включает прогнозируемые значения 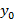с принятой доверительной вероятностью .

В случае парной регрессии можно оценить интервальное среднеквадратичное отклонение Yпрогноз по формуле

и посмотреть, попадают ли реальные значения Y в интервал Ŷ ± 2 SYпрогноз.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)