Фиктивная переменная наклона: назначение; спецификация регрессионной модели с фиктивной переменной наклона; значение параметра при фиктивной переменной. (20) стр.65

где переменная z принимает значения 0 или 1.

Фиктивные переменные позволяют объединить в одной модели выборки, имеющие отличия. В принципе, их можно рассматривать отдельно, но объединение может дать более качественную модель. Повышение качества модели можно оценить, используя тест Чоу.

В регрессионных моделях наряду с количественными переменными часто используются качественные переменные, которые выражаются в виде фиктивных (искусственных) переменных, отражающих два противоположных состояния качественного фактора. Например, D=0, если потребитель не имеет высшего образования, D=1, если потребитель имеет высшее образование. Переменная D называется фиктивной, или двоичной переменной, а также индикатором.

Регрессионные модели, содержащие лишь качественные объясняющие переменные, называются ANOVA – моделями (моделями дисперсионного анализа).

ANOVA – модели представляют собой кусочно – постоянные функции. Такие модели в экономике крайне редки. Гораздо чаще встречаются модели, содержащие как количественные, так и качественные переменные. Такие модели называются ANCOVA – моделями (моделями ковариационного анализа).

В случае, когда качественная переменная принимает не два, а большее число значений, может возникнуть ситуация, которая называется ловушкой фиктивной переменной. Она возникает, когда для моделирования k значений качественного признака используется ровно k бинарных (фиктивных) переменных. В этом случае одна из таких переменных линейно выражается через все остальные, и матрица значений переменных становится вырожденной. Тогда исследователь попадает в ситуацию совершенной мультиколлинеарности. Избежать подобной ловушки позволяет правило:

- если качественная переменная имеет k альтернативных значений, то при моделировании используется только (k-1) фиктивных переменных.

Нулевой уровень качественной переменной называется базовым или сравнительным.

Кроме того, значения фиктивных переменных можно изменять на противоположные. Суть модели от этого не изменится. Изменится только знак коэффициентаg в модели.

Коэффициент g в модели называется дифференциальным свободным членом, т.к. он показывает, на какую величину изменится свободный член модели при изменении значения фиктивной переменной.

Возможны модели, в которых используются несколько фиктивных переменных, не связанных между собой по смыслу. Тогда возможны все комбинации значений различных качественных переменных, в которых регрессии отличаются лишь свободными членами.

Подобные схемы можно распространить на произвольное число количественных или качественных факторов. При этом не следует забывать, что если качественный фактор имеет k альтернативных состояний, то для его описания можно использовать только k различных сочетаний значений (k-1) фиктивных переменных.

Влияние качественного фактора может сказываться не только на значении свободного члена, но и на угловом коэффициенте линейной регрессионной модели. Обычно это характерно для временных рядов экономических данных при изменении институциональных условий, введении новых правовых или налоговых ограничений. Тогда зависимость может быть выражена так:

где

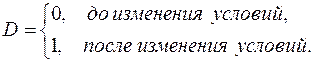
В этой ситуации ожидаемое значение зависимой переменной определяется следующим образом:

Коэффициенты g1 и g2 называются соответственно дифференциальным свободным членом и дифференциальным угловым коэффициентом. Фиктивная переменная разбивает зависимость на две части – до и после внесения изменений в условия её действия.

Общая зависимость имеет вид кусочно – линейной функции, а изменения условий отображаются изменением угла наклона прямой к оси абсцисс.

Здесь исследователь должен принять решение, стоит ли разбивать выборку на части и строить для каждой из них уравнение регрессии или ограничиться одной общей линией регрессии. Для этого используют тест Чоу, который состоит в следующем.

Вся выборка объёма n разбивается на две подвыборки объёмами n1 и n2 (n1+n2=n), и для каждой строится уравнение регрессии. Кроме того, строится общая регрессия для всех наблюдений, и для неё определяется остаточная СКО. Равенство возможно лишь при совпадении коэффициентов регрессии для всех трёх уравнений. Если сумма будет значительно меньше, то можно считать разбиение общей выборки на две подвыборки обоснованным. В этом смысле разность можно считать мерой улучшения качества модели при разбиении выборки на две части. Однако при разбиении уменьшается число степеней свободы каждой из подвыборок. Эта альтернатива между числом степеней свободы и уменьшением остаточной СКО выражается через статистику.

Поиск по сайту: