Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение. (20) с.12-21

Переменная величина х с областью изменения Х называется случайной, если в результате некоторого опыта со случайными элементарными исходами она принимает значение из множества Х, которое заранее невозможно предсказать. Случайная величина может быть дискретной или непрерывной.

Важную роль играют две количественные харак­теристики случайной переменной х: математическое ожидание (ожидаемое значение) и дисперсия. Ожидаемое зна­чение, которое обычно обозначают m, m или Е(х) находится по формуле

(2.1)

Подчеркнем, что m – это константа, вокруг которой рассеяны возможные значения q случайной переменной х.

Дисперсия s², Var(x) – это математическое ожидание квадрата отклонения случайной переменной х от её ожидаемого значения:

(2.2)

Положительный квадратный корень из дисперсии именуется средним квадратическим отклонением (СКО), или стандартным отклонением. Размерно­сти s и х совпадают. Величина s (как и s²) служит характеристикой неопределенности (изменчивости) х. Формула (2.2) может быть преобразована к виду

s ² = Е(х²) - m² (2.3)

который часто используется для расчётов вручную. Из формул (2.1) - (2.2) видно, что для отыскания величин m, s нужно знать закон распределения P_x(q) случайной пере­менной х. Часто это закон неизвестен, и тогда можно оценить (приближенно определить) характеристики m, s ² по результатам n независимых наблюдений (опытов) { х₁, х ₂, …, х_n }. В этом наборе каждая компонента х_i – это случайная пере­менная с одним и тем же законом распределения P_x(q), при этом величины х_i являются независимыми.

Что такое наилучшая оценка, или наилучшая технология оценки (estimator) математического ожидания случайной величины? Каковы её критерии?

1. Несмещенность. Применяя правильную технологию расчёта, мы не получим в результате обработки серии замеров статистически значимого отклонения от реального значения оцениваемого параметра.

2. Эффективность. среднее значение обеспечивает наиболее эффективную оценку математического ожидания Е(х). Эффективность может вступить в противоречие с несмещённостью. Например, исключение переменных из эконометрических моделей может привести к уменьшению дисперсий оцениваемых параметров и к их смещению относительно истинных значений.

3. Consistency. В российских учебниках это слово переводят как “состоятельность”, но правильнее говорить о сходимости. Это значит, что увеличивая количество замеров в серии n, мы можем получить разность оценок исследуемого параметра меньше любого e, то есть наши оценки сходятся к какому-то пределу.

41. Оценка параметров парной регрессионной модели методом наименьших квадратов с использованием сервиса Поиск решения.

Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитическая связь между ними описывается уравнениями: Прямой - , Гиперболы 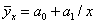, Параболы Сущность МНК заключается в нахождении параметров модели (а₀, а₁), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии: .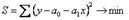

Проводят дифференцирование S по коэффицентам и приравнивают уравнения к 0. Из системы уравнений, получаем: Здесь

Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента (отношение коэффициента регрессии к его средней ошибке):

. Коэффициент регрессии считается статистически значимым, если превышает t_табл - табличное (теоретическое) значение t-критерия Стьюдента.

Проверка адекватности всей модели осуществляется с помощью F -критерия и величины средней ошибки аппроксимации .

Проверка адекватности всей модели осуществляется с помощью F -критерия и величины средней ошибки аппроксимации

Использование сервиса Поиск решения позволяет наглядно продемонстрировать суть метода наименьших квадратов (МНК). Вызывается он так же, как и Анализ данных: в Excel-2003 и более ранних версиях через меню Сервис (если не вызывается, то Сервис-На д стройки); в Excel-2007 и 2010 в меню Данные (если не вызывается, то Пуск – Параметры Excel – Надстройки – Перейти). Схема расчетов та же, что и в задачах математического программирования:

задать произвольные коэффициенты аппроксимирующей функции f(X),

построить функцию Ŷ = f(X) в заданном диапазоне Х,

вычислить отклонения Y – Ŷ для диапазона, в котором значения Y используются для настройки модели, то есть оценки коэффициентов,

вычислить все (Y – Ŷ)² и их сумму S(Y – Ŷ)² (сумма квадратов отклонений (остатков),

вызвать Поиск решения, целевая ячейка S(Y – Ŷ)², Изменяя ячейки коэффициенты, ограничений нет, Выполнить.

Метод наименьших квадратов с Поиском решения может применяться для настройки нелинейных моделей.

Показатель качества линейной модели – коэффициент корреляции Х и Y R_xy и его квадрат – коэффициент детерминации R².

Вычисленные для обеих моделей R², DW, GQ представлены в таблицах, а также показаны графики остатков. Видно, что качество обеих моделей высокое, применение МНК правомерно. Применение для прогноза одной из двух моделей зависит от дополнительной информации и личного опыта.

42. Проверка статистических гипотез, t-статистика Стьюдента, доверительная вероятность и доверительный интервал, критические значения статистики Стьюдента. Что такое “толстые хвосты”?

Инженеры считают, что размеры деталей подчиняются закону нормального распределения (ЗНР), выведенного К.Гауссом

Как видите, в функции Гаусса всего два параметра: математическое ожидание µ_х и стандартное отклонение s, которые сравнительно легко оценить по выборке, используя формулы (2.4) и (2.5). Эти формулы реализованы в Excel в функциях соответственно СРЗНАЧ, ДИСП и СТАНДОТКЛОН, категория «Статисти­ческие». Зная параметры гауссианы, можно вычислить процент деталей в различных диапазонах х (квантили), используя таблицы или функцию НОРМРАСП Excel. Поэтому закон нормального распределения широко применяется при проектировании машин и механизмов. Например, можно вычислить количество событий (деталей) в диапазоне { Е(х) -2s, Е(х) +2s}. Это примерно 95%, то есть в “хвостах” останется по 2,5%. В данном случае р = 0,95 – доверительная вероятность, а {Е(х) -2s, Е(х) +2s} - соответствующий доверительный интервал.

На Рисунке 2.2 показано применение функции НОРМРАСП. Площадь левого хвоста гауссианы (Рисунок 2.1) от - до -1,96 (почти 2) равна 0,024997895, то есть 2,5%.

В общем виде это утверждение выглядит следующим образом:

для уровня значимости a = 1– р доверительный интервал равен

{Е(х) – t_критs, Е(х) + t_критs}, где t_крит – критические значения статистики Стьюдента t = Е(х)/s. В нашем примере a – доля деталей в одном или двух “хвостах”. При уменьшении числа замеров надёжность оценки Е(х) и дисперсии падают, и доверительный интервал надо расширять. Поэтому критические значения статистики Стьюдента зависят от уровня значимости (доверительной вероятности) и количества замеров (степеней свободы). Распределение Стьюдента t _крит (a, n) приведено во всех учебниках и практикумах по математической статистике и эконометрике. В Excel имеется функция СТЬЮДРАСП(t _крит, n, число хвостов (1 или 2)), которая возвращает долю событий в одном или двух “хвостах”. Для практических целей достаточно запомнить, что при числе замеров больше 30 и р =95% t _крит примерно равно 2 (при “бесконечном” числе замеров – 1,96).

Для принятия гипотезы о влиянии регрессора на эндогенную переменную используются таблицы критических значений t-статистики Стьюдента. Для bt=b/S_b. Предполагается, что при числе измерений больше 20 истинные значения коэффициентов уравнения регрессии a и b лежат в интервалах {a-2S_a, b+2 S_b } и {b-2S_b, b+2 S_a } с доверительной вероятностью 95%.

Поиск по сайту: