Настройка модели с системой одновременных уравнений

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях - в правую часть системы:

y₁ = b_12* y₂ + b_13* y₃ +… + b_{1n *} y_n + a_{11 *} x₁ + a_{12 *} x₂ +…+ a_1m x_m + e_1,

y₂ = b_21* y₁ + b_23* y₃ +… + b_{2n *} y_n + a_{21 *} x₁ + a_{22 *} x₂ +…+ a_2m x_m + e_2,

y_n = b_n1* y₁ + b_n2* y₂ +… + b_{nn-1 *} y_n-1 + a_{n1 *} x₁ + a_{n2 *} x₂ +…+ a_nm x_m + e_n,

Система взаимозависимых уравнений получила название система совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. Экономические модели, значения переменных которых привязаны к моменту времени, называются динамическими.

Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения.

В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассм. самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные - это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через y.

Экзогенные переменные - это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.

Обозначаются через x.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Эк. переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэк. переменные (напр., климатич. условия, соц. положение, пол, возрастная категория) входят в систему только как экзогенные переменные. В качестве экзогенных переменных могут рассм. значения эндогенных переменных за предшествующий период времени (лаговые переменные).

Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения.

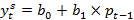
a₁<0, b₁>0

Второй пример:

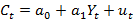
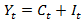
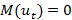
Поиск по сайту: