АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод наименьших квадратов: алгоритм метода, условия применения

Читайте также:
  1. A) подписать коллективный договор на согласованных условиях с одновременным составлением протокола разногласий
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. FAST (Методика быстрого анализа решения)
  4. I Распад аустенита в изотермических условиях
  5. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  6. I. 2.1. Графический метод решения задачи ЛП
  7. I. 3.2. Двойственный симплекс-метод.
  8. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  9. I. МЕСТО И ВРЕМЯ КАК ГРАНИЧНЫЕ УСЛОВИЯ
  10. I. Метод рассмотрения остатков от деления.
  11. I. Методические основы
  12. I. Методические основы оценки эффективности инвестиционных проектов

Для оценки параметров линейной или линеаризованной модели применяется метод наименьших квадратов (МНК). Суть метода состоит в следующем: к реальным данным подбирается функция и её параметры, чтобы разности (отклонения, остатки) между реальными и вычисленными значениями у были минимальны. Но разностей много, поэтому минимизируется сумма квадратов этих разностей:

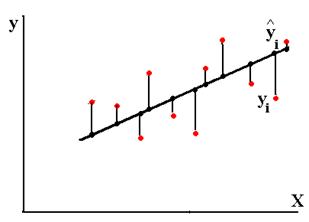
Рис.3.1. Отклонения реальных у от оценённой функции регрессии.

 

 

Как правило, вычисления проводятся на компьютере с использованием различных сервисов и программ. Далее мы рассмотрим технологию МНК, которую использовали при ручном вычислении параметров парной линейной регрессии.

Сумма квадратов остатков, зависящая от параметров a и b

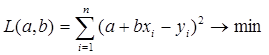
где n – количество измерений. Эта функция достигает минимума в точке, где её частные производные по a и по b равны нулю:

 

 

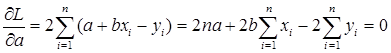
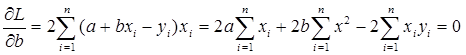
или

an + bSx = Sy

aSx + bSx2 =Sxy

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)