 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Оценка параметров парной регрессионной модели методом наименьших квадратов. (10)
Для оценки параметров линейной или линеаризованной модели применяется метод наименьших квадратов (МНК). Суть метода состоит в следующем: к реальным данным подбирается функция и её параметры, чтобы разности (отклонения, остатки) между реальными и вычисленными значениями у были минимальны. Но разностей много, поэтому минимизируется сумма квадратов этих разностей:
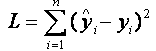
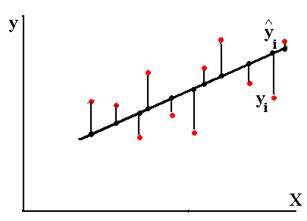
Рис.3.1. Отклонения реальных у от оценённой функции регрессии.
Как правило, вычисления проводятся на компьютере с использованием различных сервисов и программ. Далее мы рассмотрим технологию МНК, которую использовали при ручном вычислении параметров парной линейной регрессии.
Сумма квадратов остатков, зависящая от параметров a и b
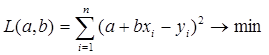
где n – количество измерений. Эта функция достигает минимума в точке, где её частные производные по a и по b равны нулю:
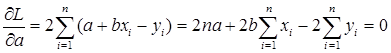
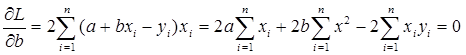
или
an + bSx = Sy
aSx + bSx2 =Sxy
Это называется система нормальных уравнений. В ней два уравнения и два неизвестных a и b, а коэффициенты получаются суммированием х, у и т.д. Решать её можно разными способами. В данном случае использован сервис Excel Поиск решения для настройки линейной модели по данным X и Y, представленным в Таблице 3.1. Коэффициенты системы нормальных уравнений расположены в виде матрицы (верхние строки таблицы 3.2), неизвестные a и b задаются произвольно и умножаются на коэффициенты (нижние строки). В окне Поиска решения задаются: Целевая ячейка – первая сумма, Значение равно 247 (Sy), Изменяя ячейки – a и b, Ограничения: вторая сумма равна 3901 (Sxy). Исходные данные X и Y приведены в Таблице 3.1. результаты расчёта в Таблице 3.2.
Таблица 3.1. Таблица 3.2.
| X | Y | X2 | XY |
| Суммы 165 |
| a | b | |
| -4,27 | 1,78 | |
| Суммы по строкам | ||
| -47,00 | 294,00 | 246,9999 |
| -705,00 | 4606,00 |
Теперь можно построить функцию регрессии Ŷ, сравнить её с Y и использовать для прогноза.
В принципе, МНК с Поиском решения можно использовать непосредственно. Для этого надо задать произвольные коэффициенты a и b, построить по ним функцию Ŷ = a + bX, вычислить остатки e = Y – Ŷ и их квадраты, сумму e 2.
В окне Поиска решения установить Целевая ячейка Se2 минимум, Изменяя ячейки a и b, ограничений нет.
Таблица 3.3.
Поиск по сайту: