АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

II Универсальная оценка остаточного члена

Читайте также:
  1. I. Оценка изменения величины и структуры имущества предприятия в увязке с источниками финансирования.
  2. I. ОЦЕНКА НАУЧНОГО УРОВНЯ ПРОЕКТА
  3. II РЕСЕНТИМЕНТ И МОРАЛЬНАЯ ОЦЕНКА
  4. II. Типы отношений между членами синтагмы
  5. III. Гигиеническая оценка условий труда
  6. III. Количественная оценка влияния показателей работы автомобиля на его часовую производительность
  7. III. Оценка давления и температуры воздуха в КС.
  8. IV. Оценка травмобезопасности рабочих мест
  9. V. ОЦЕНКА ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ
  10. XVII. Эпидемиологический анализ и оценка эффективности противоэпидемических мероприятий
  11. А) Оценка уровня подготовленности нового работника.

Остаточный член (вернее, его абсолютная величина) есть не что иное как погрешность, возникающая при замене функции её многочленом Тейлора. Именно для успешного применения формулы Тейлора в приближённых вычислениях и нужна оценка остаточного члена. Такая оценка даётся следующей теоремой.

Теорема. Пусть функция имеет в промежутке производные всех порядков, которые равномерно ограничены в совокупности, т.е. существует число такое, что Тогда для , имеем универсальную оценку:

(1)

Эта оценка сразу следует из формы Лагранжа остаточного члена и из условий теоремы.

В §6 темы «Введение в математической анализ» было доказано, что для .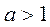

Если , то и этот предел тем более равен 0. Отсюда вытекает, что, выбирая достаточно большой номер , мы можем сделать правую часть (1) меньше любого положительного числа. Это даёт нам возможность применять формулу Маклорена для приближённого вычисления функций (удовлетворяющих условиям теоремы) с любой наперёд заданной точностью.

 

Лекция 16


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)