I Определения

Рассмотрим функцию , которая имеет в точке 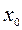производные всех порядков до п- го включительно. Составим для этой функции многочлен . (1)

Из результатов предыдущего параграфа следует, что коэффициент при 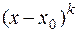, т.е. 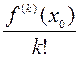, должен равняться . Таким образом, многочлен (1) удовлетворяет соотношениям:

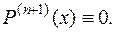
Поскольку функция не многочлен, то уже нельзя ожидать равенства . Однако, из-за совпадения производных естественно ожидать, что 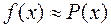. Поэтому особый интерес приобретает изучение разности

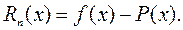
Для производных этой функции справедливы соотношения:

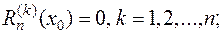
(2)

Для последнего, очевидно, требуется, чтобы у функции существовала производная 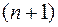-го порядка.

Принята следующая терминология:

1) многочлен (1): 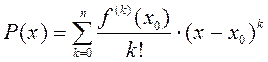– многочлен Тейлора порядка для функции ;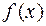

2) формула – формула Тейлора порядка для функции или разложение по формуле Тейлора функции ;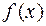

3) разность 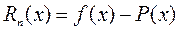– остаточный член формулы Тейлора. Для разных целей имеются различные формы остаточного члена. Формулы Тейлора и различают по этим формам. Мы рассмотрим лишь 2 формы остаточного члена.

Поиск по сайту: