АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм определения точек локальных и глобальных экстремумов функции одной переменной

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. I Определения
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. Дайте определения следующих правовых категорий.
  5. I. Деньги и их функции.
  6. I. Дифракция Фраунгофера на одной щели и определение ширины щели.
  7. I. Открытые способы определения поставщика.
  8. I. Функции
  9. I. Функции эндоплазматической сети.
  10. I.2.4. Алгоритм симплекс-метода.
  11. II. 4.1. Алгоритм метода ветвей и границ
  12. II. Исследование пульса, его характеристика. Места определения пульса.

Безусловная оптимизация функции одной переменной

1. Находится .

2. Вычисляются корни уравнения 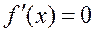− стационарные точки , где 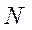− число стационарных точек. Полагается .

3. Находится .

4. Вычисляются значения 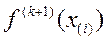для всех. . Если 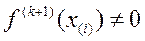, то определяется тип стационарной точки и ее номер исключается из множества .

5. Проверяется условие определения типа всех стационарных точек 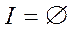. Если оно выполняется, то осуществляется переход к п.6. Если условие не выполняется, то полагается и осуществляется переход к п.3.

6. Вычисляются предельные (при и ) значения 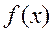. Если 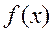не имеет конечных глобальных экстремумов, то вычисления прекращаются. В противном случае осуществляется переход к п.7.

Вычисляются значения 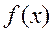на множестве точек локальных экстремумов. По наименьшему из полученных значений 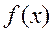определяется точка глобального минимума, по наибольшему из полученных значений 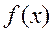− точка глобального


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)