Наибольшее и наименьшее значение функции на промежутке

Пусть функция непрерывна на замкнутом промежутке . В силу одного из свойств таких функций она достигает на этом промежутке своих наибольшего и наименьшего значений. Эти значения могут достигаться как внутри промежутка, так и на его концах. Если своего наибольшего (наименьшего) значения функция достигает во внутренней точке промежутка, то такая точка является точкой локального максимума (минимума), а значит и критической точкой первого порядка.

Можно предложить следующий алгоритм отыскания наибольшего и наименьшего значений.

1. Найти

2. Найти критические точки первого порядка и отобрать из них те, которые лежат внутри промежутка .

3. Вычислить значения функции в точках, полученных в предыдущем пункте, а также на концах отрезка.

4. Из ряда чисел, полученных в предыдущем пункте, выбрать наибольшее и наименьшее: они и являются соответственно наибольшим и наименьшим значениями функции на промежутке .

Пример 1. Найдем наибольшее и наименьшее значения функции на промежутке

Решение. 1) Находим производную: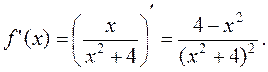

2) Находим критические точки. В данном случае – это только решения уравнения , т.к. производная существует всюду:

3) Вычисляем значения функции:

4)

Замечание. В случае исследования функции , непрерывной на открытом промежутке , вместо значений и вычисляют односторонние пределы , .

Рассмотрим два примера, в которых приходится находить наименьшее или наибольшее значения некоторых функций. Впрочем, чаще всего интерес представляют не столько сами эти значения, а те значения аргумента, которые доставляют их функции.

Пример 2. Из квадратного листа жести со стороной , вырезая по углам равные квадраты и сгибая края, составляют прямоугольную открытую сверху коробку. Как получить коробку наибольшего объёма?

Решение. Обозначим сторону вырезаемого квадрата через . Тогда основание коробки – это квадрат со стороной и её объём 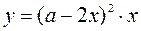, при этом изменяется в промежутке . Вопрос свёлся к нахождению наибольшего значения функции на указанном промежутке:

1)

2)

3)

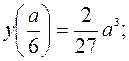
4) Наибольшая вместимость коробки получится, если сторона вырезаемого квадрата составляет часть стороны исходного.

Пример 3. Через фиксированную точку внутри угла провести прямую, отсекающую от угла треугольник наименьшей площади.

Решение.

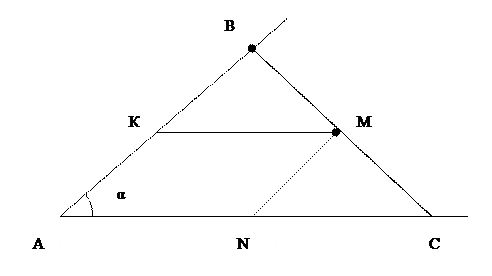
Пусть и – точки пересечения искомой прямой со сторонами угла. Требуется минимизировать площадь .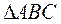

Проведём отрезки и . Их длины обозначим через и 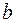соответственно (это фиксированные числа, ибо точка фиксированная). В качестве аргумента минимизируемой функции возьмём длину отрезка . Очевидно, . Из подобия 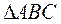и имеем: Площадь треугольника вычисляем по формуле

Итак, минимизируемая функция имеет вид: где

1)

2)

3) Так как при и 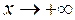функция , то в единственной критической точке (из области определения функции) имеем минимум.

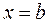4) Наименьшее значение площадь треугольника принимает при , т.е. прямую надо проводить так, чтобы отрезок 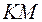(и ) был средней линией 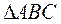. Другими словами, прямую через точку надо проводить так, чтобы отрезок, заключённый между сторонами угла, делился в точке пополам.

Тема ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА

Лекция 15

Поиск по сайту: