АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Разложение по формуле Маклорена некоторых элементарных функций

Читайте также:
  1. I. Составление дифференциальных уравнений и определение передаточных функций
  2. II. ЦАРСТВО ЭЛЕМЕНТАРНЫХ СУЩЕСТВ
  3. IIІ Исследование функций
  4. Ms Excel: мастер функций. Логические функции.
  5. Автоматизация функций в социальной работе
  6. Алгоритм метода сопряжённых направлений Пауэлла для оптимизации квадратичных функций.
  7. Алгоритм построения графиков функций вида
  8. АНАЛИЗ ФУНКЦИЙ СПЕЦИАЛИСТОВ ПО СТРАТЕГИЧЕСКОМУ МЕНЕДЖМЕНТУ И ПОЛНОМОЧИЙ ОРГАНОВ УПРАВЛЕНИЯ ОРГАНИЗАЦИИ, ПРИНИМАЮЩИХ СТРАТЕГИЧЕСКИЕ РЕШЕНИЯ.
  9. Анализ функций управления
  10. Анатомо-физиологические основы саморегуляции функций организма.
  11. Аргументы финансовых функций Excel анализа инвестиций
  12. Аргументы финансовых функций Excel анализа ценных бумаг

 

I. .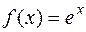

Поскольку 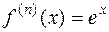и , то формула Маклорена имеет вид

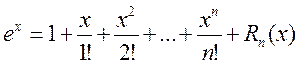
где: 1)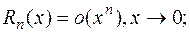

2) 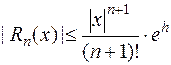, для любого промежутка 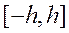(очевидно, что ).

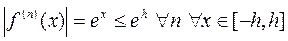II. .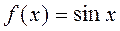

Известно, что 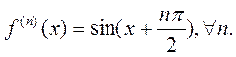Тогда:

Условия теоремы из §3 выполнены на всей оси с 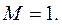Формула Маклорена имеет вид

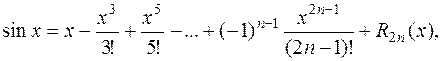
где: 1)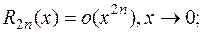

2) .

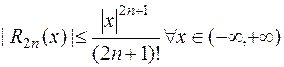На первый взгляд написанные формы для 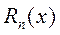отличаются от общих результатов. Но надо не забывать, что, вообще говоря, в разложении для можно дописать ещё один член с 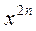, только коэффициент при этой степени равен 0.

 

III. .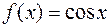

Аналогично предыдущему нетрудно получить

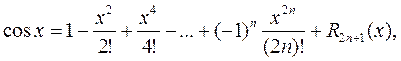
где: 1)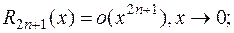

2) .

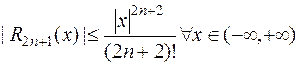IV. .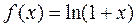

Прежде всего, имеем 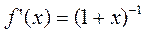. Теперь можно использовать формулу дифференцирования степенной функции:

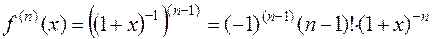
При 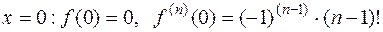Формула Маклорена имеет вид (с учётом того, что ):

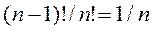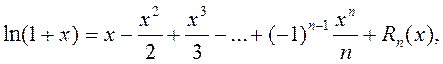
где: 1)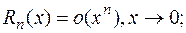

2)

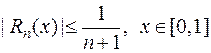
Отметим, что для оценки остаточного члена для 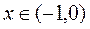требуется форма 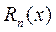, отличная от формы Пеано и Лагранжа. Кроме того, пользоваться разложением 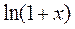в приближённых вычислениях можно только для : только для таких значений .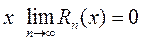

 

V. .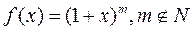

Поскольку

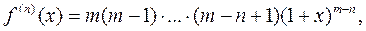то

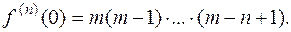
Формула Маклорена для этой функции имеет вид:

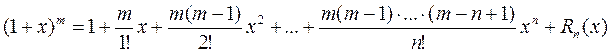Здесь для остаточного члена имеем: 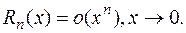Как и в случае логарифмической функции для оценки 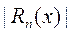требуется форма, отличная от Пеано и Лагранжа. Более подробно об этом мы будем говорить в третьем семестре в теме «Степенные ряды». Отметим только, что написанным разложением в приближённых вычислениях можно пользоваться лишь для .

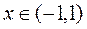VI. Другие функции. Пользуясь известными разложениями, можно, не вычисляя производных, непосредственно писать разложения с остаточным членом в форме Пеано и для более сложных функций. При этом все степени х, до назначенной включительно, учитываем точно, а более высокие степени будем сразу включать в 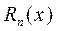(не выписывая их).

Пример 1. Написать разложении функции 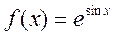до .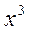

В силу I имеем:

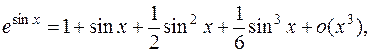где остаточный член

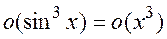, так как 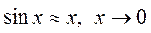. Далее, в силу II имеем: . Таким образом

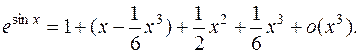
После упрощения получим искомое разложение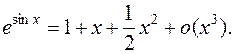

Пример 2. Написать разложение функции 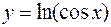до члена с .

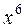Согласно IV,

.

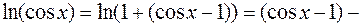
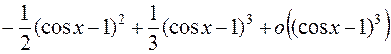Необходимое разложение для (см. III) выпишем в нескольких вариантах:

.

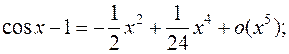
Учитывая, кроме всего, и 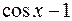~ –0,5 х 2, х → 0, получим:

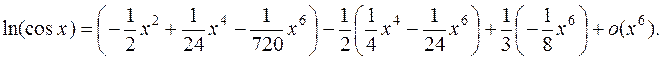
После приведения подобных членов будем иметь:

.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

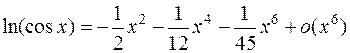Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)