АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм метода сопряжённых направлений Пауэлла для оптимизации квадратичных функций

Читайте также:
  1. I.2.4. Алгоритм симплекс-метода.
  2. II. 4.1. Алгоритм метода ветвей и границ
  3. II. Проблема источника и метода познания.
  4. LU – алгоритм нахождения собственных значений для несимметричных задач
  5. Ms Excel: мастер функций. Логические функции.
  6. QR- алгоритм нахождения собственных значений
  7. SALVATOR - это переход физического явления в семантико-нейронный алгоритм (инструкцию) освобождения человека от негативных последствий этого явления.
  8. SWOT-анализ в качестве универсального метода анализа.
  9. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
  10. Административными методами можно предотвратить необоснованные расходы (хищение, злоупотребление).
  11. Алгоритм
  12. Алгоритм

Начальный этап. Задать начальную точку 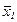и систему 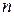линейно-независимых направлений , 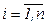(например, ), положить , .

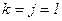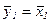Основной этап.

Шаг 1. Положить , , .

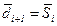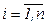Шаг 2. Вычислить , .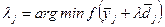

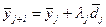Шаг 3. Если , то положить и перейти к шагу 2.

Шаг 4. Положить , .

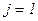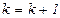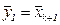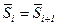Шаг 5. Если , то положить , , , , , и перейти к шагу 1.

Шаг 6. Вычислить , положить 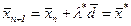и остановиться.

Из теоремы 3.3 следует, что приведённый алгоритм генерирует сопряжённые направления. Для того чтобы воспользоваться теоремой 3.1, необходимо дополнить алгоритм Пауэлла процедурой проверки линейной независимости генерируемых алгоритмом направлений.

Алгоритм метода Пауэлла для оптимизации неквадратичных функций

Начальный этап. Задать начальную точку 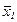, 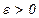- параметр окончания счёта и систему 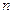линейно-независимых направлений , , 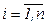положить , .

Основной этап.

Шаг 1. Положить , , .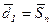

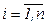Шаг 2. Вычислить , .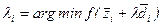

Шаг 3. Если 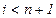, то положить и перейти к шагу 2.

Шаг 4. Положить , , , , .

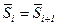Шаг 5. Если , то положить 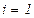, , , перейти к шагу 1.

Шаг 6. Вычислить , .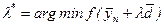

Шаг 7. Если , то 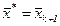и остановиться, иначе положить 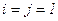, , 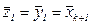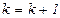и перейти к шагу 1.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)