АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Функция Лагранжа. Седловая точка функции Лагранжа, необходимые и достаточные условия её существования (общий случай)

Читайте также:
  1. A) подписать коллективный договор на согласованных условиях с одновременным составлением протокола разногласий
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. I Психологические принципы, задачи и функции социальной работы
  4. I Распад аустенита в изотермических условиях
  5. I Функция
  6. I. Деньги и их функции.
  7. I. МЕСТО И ВРЕМЯ КАК ГРАНИЧНЫЕ УСЛОВИЯ
  8. I. Неблагоприятные условия для жизни бактерий создаются при
  9. I. Необходимые документы для участия в Конкурсе
  10. I. Правила поведения в условиях вынужденного автономного существования.
  11. I. При каких условиях эта психологическая информация может стать психодиагностической?
  12. I. Психологические условия эффективности боевой подготовки.

Определение 5.1. Функция , (3.6)

где , называется функцией Лагранжа для задачи выпуклого программирования (10.4), (10.5).

Определение 5.2. Точка называется седловой точкой функции Лагранжа (10.10) на множестве , , если

1) , , (3.7)

2) для всех , .

Соотношение (3.7) можно переписать следующим образом:

(3.8)

В задачах выпуклого (и, в частности, квадратичного и линейного программирования) функция Лагранжа играет важную роль, а именно при довольно общих предположениях задача выпуклого программирования сводится к отысканию седловых точек функции Лагранжа. “Простые” же ограничения задачи (3.8) позволяют применять для ее решения методы, схожие с численными методами безусловной оптимизации.

Следующая теорема дает другое, равносильное (3.7), определения седловой точки.

Теорема 2.1. для того чтобы точка 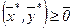была седловой точкой функции Лагранжа, необходимо и достаточно, чтобы выполнялись следующие условие:

(3.9)

для всех , , , .

 


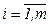1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)