Методы нулевого порядка

Для реализации методов прямого поиска требуются только значения целевой функции и не требуются значения ее производных (т.е. степень гладкости – нулевая). Очевидно, что методы прямого поиска можно применять для решения тех задач (5.1), в которых является гладкой и даже дважды гладкой, например, в тех случаях, когда вычисление производных затруднительно.

Методы прямого поиска можно разделить на эвристические и теоретические. Эвристические методы реализуют процедуры поиска с помощью интуитивных представлений, тогда как теоретические методы основаны на соответствующей математической теории.

К эвристическим методам относятся, например, метод поиска по симплексу ( - метод), метод Нелдера-Мида (метод деформируемого многогранника), метод Хука-Дживса. В данном разделе будет рассмотрен метод Хука-Дживса. К теоретическим методам нулевого порядка можно отнести, например, метод покоординатного спуска и его различные модификации, рассматриваемые в данном разделе, метод сопряженных направлений Пауэлла, который будет рассмотрен далее, и другие. К числу положительных свойств методов прямого поиска следует отнести относительную простоту вычислительных процедур, легкую машинную реализацию. С другой стороны, реализация методов нулевого порядка требует более значительных временных затрат по сравнению с методами высших порядков.

1.5.2.1. Метод Хука-Дживса

Этот метод был разработан в 1961 году для решения задачи (5.1). Метод Хука-Дживса представляет собой последовательность двух процедур: исследующего поиска (ИП) вокруг текущей базисной точки и поиска по образцу (ПО).

Исследующий поиск (ИП). Для проведения ИП необходимо задать исходную базисную точку , шаг для каждой переменной , - коэффициент уменьшения шага в процессе поиска. Каждая переменная (координата) по очереди изменяется на величину шага и вычисляется , где - j -ый единичный вектор . Если , то заменяется на . В противном случае делается шаг в противоположном направлении, т.е. вычисляется . Если это приводит к уменьшению значения функции, то 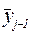заменяется на ; иначе точка не заменяется. После перебора всех n координат ИП вокруг точки завершается получением новой базисной точки . Если новая базисная точка , производится поиск по образцу, иначе ИП повторяется вокруг точки , но с уменьшенным шагом.

Алгоритм исследующего поиска вокруг текущей базисной точки x

Начальный этап. Задать точку , систему линейно-независимых направлений , шаг ; положить , ; .

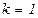Основной этап.

Шаг 1. Вычислить , .

Шаг 2. Если , то перейти к шагу 5.

Шаг 3. Вычислить , .

Шаг 4. Если , то перейти к шагу 5, иначе положить , .

Шаг 5. Если , то положить 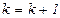и перейти к шагу 1, иначе положить и остановиться.

Поиск по образцу (ПО) заключается в нахождении точки , лежащей на направлении, соединяющем две соседние базисные точки и : .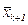

Далее проводится ИП вокруг точки , приводящий в точку . Если , то точка принимается за новую базисную точку 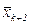и вновь производится ПО, но уже в направлении , в противном случае нужно вернуться в точку 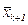и провести ИП вокруг нее с целью построения нового направления движения по образцу. Если ИП вокруг текущей базисной точки не приводит к успеху 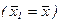, т.е. значение функции не уменьшается при движении вдоль любых координат осей, то необходимо уменьшить величину шага вдоль каждой из осей и провести ИП заново. Решение задачи завершается, когда величина шага () становится достаточно малой.

Поиск по сайту: