Критерии выпуклости (вогнутости) функций

Непрерывно-дифференцируемую на множестве 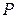функцию 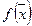будем называть гладкой функцией. Множество таких функций принято обозначать через .

Дважды непрерывно-дифференцируемую функцию будем называть дважды гладкой.

Теорема 1.8. Пусть 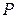– выпуклое множество, функция 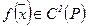. Для того чтобы 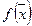была вогнута (выпукла) на 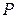, необходимо и достаточно выполнение неравенства 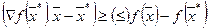, для всех 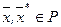(2.3)

Теорема 1.9. Пусть 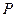– выпуклое множество, функция . Тогда, для того чтобы 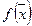была вогнута (выпукла) на 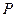, необходимо и достаточно выполнение неравенства 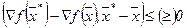для всех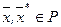

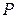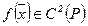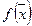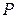Теорема 1.10. Пусть – выпуклое множество из , , функция . Тогда для вогнутости (выпуклости) на необходимо и достаточно выполнение неравенства

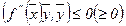(2.4)

для всех 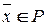и , где

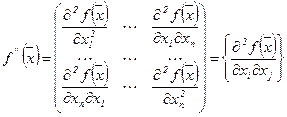(2.5)

Замечание. Условие (2.4) представляет собой условие неположительности квадратичной формы на :

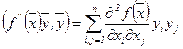. (2.6)

Существует алгебраический критерий неположительности квадратичной формы: для того чтобы квадратичная форма 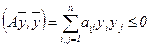для всех 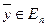, необходимо и достаточно, чтобы все главные миноры матрицы 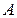имели следующие знаки:

(2.7)

Условие 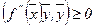– условие неотрицательности квадратичной формы.

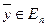Алгебраический критерий неотрицательности квадратичной формы: для того чтобы выполнялось условие квадратичной формы для всех , необходимо и достаточно, чтобы все главные миноры матрицы 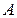были неотрицательны

. (2.8)

Неравенство (2.4) является удобным средством проверки вогнутости (выпуклости) дважды гладких функций.

Поиск по сайту: