АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Экстремальные свойства выпуклых (вогнутых) функций

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. I. Составление дифференциальных уравнений и определение передаточных функций
  3. II. Свойства векторного произведения
  4. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  5. IIІ Исследование функций
  6. Ms Excel: мастер функций. Логические функции.
  7. V2: Электрические и магнитные свойства вещества
  8. Автоматизация функций в социальной работе
  9. Аксиомы ординалистского подхода. Функция полезности и кривые безразличия потребителя. Свойства кривых безразличия. Предельная норма замещения
  10. Акустические свойства голоса
  11. Акустические свойства горной породы.
  12. Акустические свойства строительных материалов

Определение 4.1. Функция 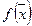достигает на замкнутом множестве в точке глобального максимума, если 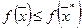для всех .

Определение 4.2. Функция достигает на замкнутом множестве в точке локального максимума, если существует число такое, что для всех , где

Для функции, график которой изображен на рис.1, точки , , , являются точками локального максимума, – точка глобального максимума.

Рисунок 1.

Теорема 1.11. Пусть множество 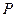выпукло, а функция 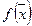определена и вогнута на 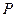тогда:

1) всякий локальный максимум этой функции является и глобальным максимумом этой функции;

2) множество точек глобальных максимумов является выпуклым множеством, т.е. – выпуклое множество;

3) если 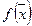строго вогнута на 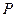, то содержит не более одной точки.

Теорема 1.12. Критерий оптимальности для вогнутых функций.

Пусть 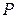– выпуклое множество, функция , . Тогда в любой точке необходимо выполняется неравенство

(2.9)

для всех . Причем, если , то неравенство (2.9) обращается в равенство . Если 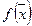вогнута на 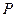, то условие (2.9) является достаточным для того, чтобы .

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)