 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Алгоритм метода покоординатного спуска, не использующий одномерной оптимизации
Первый вариант
Начальный этап. Задать начальную точку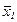 
, 
– параметр окончания счета, 
– первоначальная величина шага, 
– коэффициент уменьшения шага, положить 
, 
.
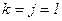Основной этап.
Шаг 1. Вычислить 
.
Шаг 2. Если 
, то перейти к шагу 5.
Шаг 3. Вычислить 
.
Шаг 4. Если , то перейти к шагу 5, иначе положить 
.
Шаг 5. Если 
, то положить 
и перейти к шагу 1.
Шаг 6. Положить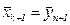 
.
Шаг 7. Если 
, то перейти к шагу 9, иначе перейти к шагу 8.
Шаг 8. Если 
, то положить 
и остановиться, иначе положить 
, 
, 
и перейти к шагу 1.
Шаг 9. Если 
, то положить 
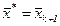и остановиться, иначе положить 
, , 
и перейти к шагу 1.
Второй вариант
Начальный этап. Такой же, как в первом варианте.
Основной этап.
Шаг 1. Вычислить .
Шаг 2. Если , то перейти к шагу 6.
Шаг 3. Вычислить .
Шаг 4. Если , то перейти к шагу 6.
Шаг 5. Если , то перейти к шагу 6, иначе положить и перейти к шагу 1.
Шаг 6. Если 
, то положить и перейти к шагу 1.
Шаг 7. Положить .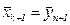
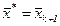Шаг 8. Если , то положить и остановиться, иначе положить , , и перейти к шагу 1.
Если пользоваться терминологией Хука-Дживса, то метод покоординатного спуска, не использующий одномерной оптимизации, состоит из последовательности ИП вокруг текущей (базисной) точки и не предполагает поиска по образцу, что во многих случаях замедляет сходимость. ИП вокруг текущей точки 
состоит из n- итераций, каждая из которых состоит из поиска точки на соответствующей координатной оси 
. Величина шага вдоль оси определяется так называемым методом удвоения (название метода соответствует случаю, когда 
; 
). В первом варианте алгоритма величина шага вдоль оси остается постоянной при проведении ИП вокруг текущей точки и уменьшается лишь тогда, когда ИП не приводит к уменьшению значения функции 
. Во втором варианте алгоритма величина шага может меняться при поиске вдоль каждой из координатных осей, причем как в сторону уменьшения шага (), если значение функции не уменьшилось, так и в сторону увеличения шага (), если значение функции уменьшилось, причем процесс увеличения продолжается до тех пор, пока убывание функции не прекратится.
Поиск по сайту: