АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема Куна-Таккера: общий случай

Читайте также:
  1. I. 4.1. Первая теорема двойственности
  2. III Общий порядок перемещения товаров через таможенную границу Таможенного союза
  3. S-M-N-теорема, приклади її використання
  4. Б1 1.Системы линейных алгебраических уравнений (СЛУ). Теорема Кроникера-Капелли. Общее решение СЛУ.
  5. Базисный минор и ранг матрицы. Теорема о базисном миноре
  6. Билет 22Понятие евклидова пространства, неравенство Коши-Буняковского. Теорема Кронекера Капелли.
  7. Билет 5 Теорема Безу и следствия из неё. Основная теорема алгебры.
  8. Важность вопроса: общий взгляд на стресс.
  9. Внешние эффекты (экстерналии). Теорема Коуза.
  10. Внешние эффекты и внешние затраты. Государственная политика в случаях их возникновения. Теорема Коуза.
  11. Внешние эффекты трансакционные издержки. Теорема Коуза
  12. Внешние эффекты, их виды и последствия. Теорема Коуза

Теорема 2.5. Если в задаче выпуклого программирования (3.4)-(3.5) множество 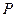обладает свойством регулярности, то необходимым и достаточным условием оптимальности точки является существование такого , что точка является седловой точкой функции Лагранжа на множестве , .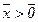

Если в задаче выпуклого программирования (3.4), (3.5) функци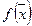и и 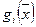, 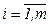являются непрерывно дифференцируемыми, то теоремы 2.2. и 2.5. можно объединить в одну (теорема 2.6).

Теорема 10.6. Если в задаче выпуклого программирования (3.4), (3.5) множество 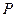обладает свойствами регулярности, то необходимым и достаточным условием оптимальности точки является существование такого , что для точки выполняются условия (3.10)-(3.15).

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)