АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод покоординатного спуска

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. Метод рассмотрения остатков от деления.
  8. I. Методические основы
  9. I. Методические основы оценки эффективности инвестиционных проектов
  10. I. Организационно-методический раздел
  11. I. Предмет и метод теоретической экономики
  12. I. Что изучает экономика. Предмет и метод экономики.

В этом методе в качестве направлений поиска используются координатные векторы 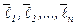, вследствие чего у текущей точки на каждой итерации изменяется лишь одна координата. Существуют многочисленные варианты покоординатного спуска, в частности использующие и не использующие методы одномерного поиска.

Алгоритм метода циклического покоординатного спуска,
использующий одномерный поиск

Начальный этап. Задать начальную точку 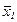, 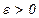– параметр окончания счета, положить , .

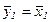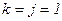Основной этап.

Шаг 1. Вычислить .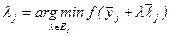

Шаг 2. Положить .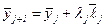

Шаг 3. Если 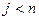, то положить , перейти к шагу 1, иначе положить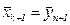

Шаг 4. Если 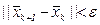, то положить 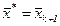и остановиться, иначе положить 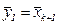, , 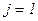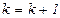и перейти к шагу 1.

Очевидно, что рассмотренный выше алгоритм Хука-Дживса, использующий одномерный поиск, является модификацией метода покоординатного спуска. Эта модификация за счет проведения поиска вдоль направления 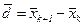существенно ускоряет сходимость метода, особенно в тех случаях, когда линии уровня функции 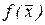искривлены или растянуты.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)