АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Оптимизация квадратичной функции

Читайте также:
  1. F полезности и ее оптимизация
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. Деньги и их функции.
  5. I. Функции
  6. I. Функции эндоплазматической сети.
  7. II. Основные задачи и функции
  8. II. Основные задачи и функции
  9. II. Функции плазмолеммы
  10. III. Предмет, метод и функции философии.
  11. III. Функции и полномочия Гостехкомиссии России
  12. IV. Конструкция бент-функции

Рассмотрим задачу безусловной оптимизации квадратичной функции

, (5.3)

где , , – симметричная матрица порядка .

Задачи оптимизации квадратичных функций занимают важное место в теории оптимизации в силу следующих причин:

1. Квадратичная функция представляет собой простейший тип нелинейной функции, для которой может быть поставлена задача безусловной оптимизации.

2. Решение задачи безусловной оптимизации может быть получено не более чем за 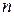шагов при условии, что поиск ведется вдоль сопряженных относительно матрицы направлений.

3. Поскольку в окрестностях точки оптимума произвольную нелинейную функцию можно достаточно хорошо аппроксимировать квадратичной функцией, то естественно ожидать, что алгоритмы, использующие сопряженные направления, будут эффективны и для оптимизации неквадратичных функций.

Основная идея алгоритмов, использующих сопряженные направления, заключается в связи между построением указанных направлений и преобразованием квадратичных функций к виду полных квадратов.

Теорема 3.1. Пусть задача (5.3) решается с помощью следующего алгоритма:

Начальный этап. Задать – произвольную начальную точку, 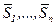– – сопряженные направления, положить .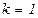

Основной этап.

Шаг 1. Определить , .

Шаг 2. Положить ;

Шаг 3. Если , то положить 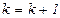и перейти к шагу 1, иначе положить и остановится.

Тогда , где .

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)