Описание и алгоритм метода

К задачам квадратичного программирования относят специальный класс задач НП, для которых целевая функция - квадратичная и вогнутая (или выпуклая), а все ограничения линейны.

Применив к этой задаче теорему Куна-Таккера, получим условия для оптимального решения в виде системы линейных уравнений, решить которые можно симплекс-методом.

В матричном виде эта задача записывается так:

максимизировать

(5.5.1)

при ограничениях

(5.5.2)

где – симметричная, отрицательно определенная матрица,

Заметим, что если – отрицательно определенная матрица, то квадратичная форма вогнута (выпукла вверх). Следовательно, задача (5.5.1), (5.5.2) является задачей вогнутого программирования.

Приведем примеры квадратичных функций:

Будем предполагать, что - строго вогнута. Применив к задаче (5.5.1) – (5.5.2) теорему Куна-Таккера, получим необходимые и достаточные условия оптимальности в виде теоремы [18; 23].

Теорема 5.14. Вектор является оптимальным решением задачи квадратичного программирования тогда и только тогда, когда существуют такие 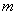-мерные вектора и -мерный вектор , что выполняются следующие условия:

Заметим, что условия 1), 2) образовывают относительно переменных 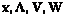систему уравнений с неизвестными.

Поиск по сайту: