АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема Куна-Таккера: случай линейных ограничений

Читайте также:
  1. I. 4.1. Первая теорема двойственности
  2. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  3. I.СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. МЕТОД ГАУССА
  4. S-M-N-теорема, приклади її використання
  5. V2: ДЕ 55 - Решение линейных неоднородных уравнений со специальной правой частью
  6. А. Простая, единичная, или случайная, форма стоимости
  7. Автокорреляция случайного возмущения. Причины. Последствия.
  8. Алгоритм решения линейных неоднородных ДУ с постоянными коэффициентами
  9. Алгоритм решения систем линейных уравнений методом Жордана-Гаусса
  10. Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.
  11. Б1 1.Системы линейных алгебраических уравнений (СЛУ). Теорема Кроникера-Капелли. Общее решение СЛУ.
  12. Базисный минор и ранг матрицы. Теорема о базисном миноре

Рассмотрим следующую задачу выпуклого программирования

, (3.25)

, (3.26)

где 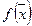– вогнутая функция, , , 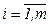– заданные векторы.

Оказывается, если ограничения, задающие множество 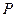, линейны, то теоремы (2.5) и (2.6) справедливы без предположения о регулярности множества .

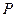Теорема 2.7. Для того чтобы точка была решением задачи (3.25), (3.26), необходимо и достаточно существование такого , чтобы точка была седловой точкой функции Лагранжа задачи выпуклого программирования (3.25)-(3.26).

Теорема 2.8. Для того чтобы точка была решением задачи (3.25), (3.26), необходимо и достаточно существование такого , чтобы для точки выполнялись условия (3.10)-(3.15).

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)