АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Постановка задачи. Задачей многомерной безусловной оптимизации функции нескольких переменных будем называть задачу, в которой требуется найти

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  7. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  8. I. Ситуационные задачи и тестовые задания.
  9. I. Цель и задачи дисциплины
  10. I.5.3. Подготовка данных для задачи линейного программирования
  11. I.5.4. Решение задачи линейного программирования
  12. I.5.5. Просмотр и анализ результатов решения задачи

Задачей многомерной безусловной оптимизации функции нескольких переменных будем называть задачу, в которой требуется найти

, (5.1)

при отсутствии ограничений на ,

где – вектор управляемых переменных,

– скалярная целевая функция.

Определение 7.1. Решением или точкой минимума задачи безусловной оптимизации будем называть такой вектор , что для всех , и писать

, (5.2)

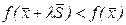Определение 7.2. Вектор называется направлением спуска функции в точке , если существует такое , что для всех .

Сущность рассматриваемых в данном разделе методов решения задачи (5.1) состоит в построении последовательности точек , принадлежащих , монотонно уменьшающих значения функции . Такие методы называют методами спуска.

Алгоритм метода спуска

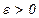Начальный этап. Задать – начальную точку, -параметр окончания счета, положить .

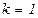Основной этап.

Шаг 1. В точке проверить условие окончания счета; если оно выполняется, то положить и остановиться.

Шаг 2. В точке выбрать направление спуска .

Шаг 3. Положить , где – длина шага вдоль направления , положить 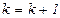и перейти к шагу 1.

Различные методы спуска отличаются друг от друга способом выбора направления спуска и шага вдоль этого направления . Естественно, что трудоемкость вычисления величины следует согласовывать с трудоемкостью определения направления спуска .

Методы решения задач безусловной оптимизации можно разделить на группы в зависимости от уровня используемой в методе информации о целевой функции, например:

1. методы нулевого порядка, или прямого поиска, основанные на вычислении только значений функции;

2. градиентные методы, в которых используются значения функции и ее градиента, т.е. вектора, компонентами которого являются частные производные первого порядка;

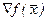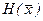3. методы второго порядка, в которых используются первые и вторые производные функции , т.е. значения , , и , где 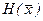- матрица Гессе, элементами которой являются частные производные второго порядка функции ;

4. методы оптимизации квадратичных функций.

Первые три группы методов различаются требуемой степенью гладкости целевой функции (разрывная, непрерывная, непрерывно-дифференцируемая, дважды непрерывно-дифференцируемая), тогда как вид самой функции не оговаривается, четвертая группа ориентирована на оптимизацию функции определенного вида.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)