АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определения

Читайте также:
  1. I Определения
  2. I. Дайте определения следующих правовых категорий.
  3. I. Открытые способы определения поставщика.
  4. II. Исследование пульса, его характеристика. Места определения пульса.
  5. III. Используемые определения и обозначения
  6. Алгоритм определения валютно-правового статуса ценных бумаг
  7. Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами.
  8. Алгоритм определения предпочтительной организационной структуры управления диверсифицированной фирмы
  9. Алгоритм определения точек локальных и глобальных экстремумов функции одной переменной
  10. Анализ порядка определения и формирования цены ДР.
  11. АНКЕТА ОПРЕДЕЛЕНИЯ ВОЛЕВЫХ КАЧЕСТВ У УЧАЩИХСЯ 12-16 ЛЕТ
  12. АНКЕТА ОПРЕДЕЛЕНИЯ ВОЛЕВЫХ КАЧЕСТВ У УЧАЩИХСЯ 16 ЛЕТ И СТАРШЕ И СТУДЕНТОВ

Определение 2.1. Функция , определенная на выпуклом множестве , называется вогнутой (выпуклой) на этом множестве, если

(2.1)

для всех 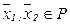и всех , .

Определение 2.2. Если для любого неравенство выполняется как строгое, то функция называется строго вогнутой (выпуклой) на .

Функция является выпуклой (строго выпуклой) на выпуклом множестве , если вогнута (строго вогнута) на множестве .

Замечание 2.1. Если множество пусто или состоит из одной точки, то функцию можно считать вогнутой (выпуклой) по определению.

Замечание 2.2. Линейная функция на всем пространстве является одновременно и вогнутой и выпуклой.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)