АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод Пауэлла

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. Метод рассмотрения остатков от деления.
  8. I. Методические основы
  9. I. Методические основы оценки эффективности инвестиционных проектов
  10. I. Организационно-методический раздел
  11. I. Предмет и метод теоретической экономики
  12. I. Что изучает экономика. Предмет и метод экономики.

Рассмотрим задачу (5.3) и метод её решения, предложенный Пауэллом в 1964 году. Метод Пауэлла представляет собой алгоритм построения системы сопряжённых направлений с использованием только значений целевой функции. Построение сопряжённых направлений основано на следующем свойстве квадратичных функций.

Теорема 3.2. Пусть - квадратичная функция, - две произвольные точки, - произвольное направление. Далее пусть и , . Тогда направление сопряжено с , т.е.

.

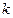Теорема 3.3. Пусть - точка, найденная в результате поиска из точки вдоль каждого из - сопряжённых направлений , а точка получена в результате поиска из точки вдоль те же направлений. Тогда направление сопряжено со всеми направлениями .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)