АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм метода ДФП

Читайте также:
  1. I.2.4. Алгоритм симплекс-метода.
  2. II. 4.1. Алгоритм метода ветвей и границ
  3. II. Проблема источника и метода познания.
  4. LU – алгоритм нахождения собственных значений для несимметричных задач
  5. QR- алгоритм нахождения собственных значений
  6. SALVATOR - это переход физического явления в семантико-нейронный алгоритм (инструкцию) освобождения человека от негативных последствий этого явления.
  7. SWOT-анализ в качестве универсального метода анализа.
  8. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
  9. Административными методами можно предотвратить необоснованные расходы (хищение, злоупотребление).
  10. Алгоритм
  11. Алгоритм
  12. Алгоритм

Начальный этап.

Задать начальную точку 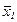и симметрическую положительно определённую матрицу . Положить 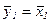, 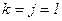. Задать 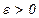- параметр окончания счёта.

Основной этап.

Шаг 1. Вычислить .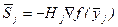

Шаг 2. Вычислить , положить .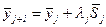

Шаг 3. Если 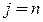, то перейти к шагу 5.

Шаг 4. Вычислить , ,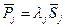

;

,

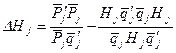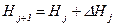положить и перейти к шагу 1.

Шаг 5. Положить 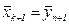. Если 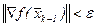, то положить 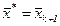и остановиться, иначе положить 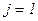, , 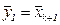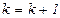и перейти к шагу 1.

В условиях алгоритма ДФП справедлива теорема.

Теорема 3.4. Направления 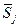(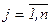), генерируемые алгоритмом ДФП, являются направлениями спуска, а матрицы 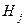(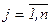)- симметрическими и положительно определёнными.

Теперь рассмотрим задачу безусловной оптимизации квадратичной функции:

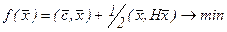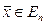, , (5.4)

где 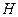- симметрическая положительно определённая матрица.

 

Теорема 3.5. Пусть задача (5.4) решается методом ДФП. Тогда, если 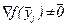для всех j, то

1) направления 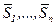являются 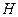- сопряжёнными;

2) 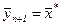-является решением задачи;

3) .

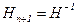Из теоремы 3.5. следует, что задача (5.4) с помощью алгоритма ДФП решается за одну итерацию .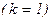

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)