АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм метода Флетчера-Ривса

Читайте также:
  1. I.2.4. Алгоритм симплекс-метода.
  2. II. 4.1. Алгоритм метода ветвей и границ
  3. II. Проблема источника и метода познания.
  4. LU – алгоритм нахождения собственных значений для несимметричных задач
  5. QR- алгоритм нахождения собственных значений
  6. SALVATOR - это переход физического явления в семантико-нейронный алгоритм (инструкцию) освобождения человека от негативных последствий этого явления.
  7. SWOT-анализ в качестве универсального метода анализа.
  8. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
  9. Административными методами можно предотвратить необоснованные расходы (хищение, злоупотребление).
  10. Алгоритм
  11. Алгоритм
  12. Алгоритм

Начальный этап. Задать начальную точку 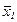, 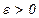- параметр окончания счёта, положить , , .

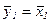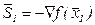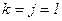Основной этап.

Шаг 1. Если 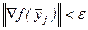, то положить 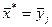и остановиться.

Шаг 2. Вычислить , положить .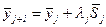

Шаг 3. Если 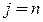, то перейти к шагу 5.

Шаг 4. Вычислить 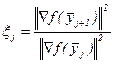и 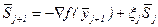, положить и перейти к шагу

Шаг 5. Положить 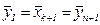, , 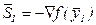, 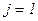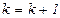и прейти к шагу 1.

Рассмотрим применение метода Флетчера-Ривса к задаче (5.4).

Теорема 3.6. Пусть задача (5.4) решается методом Флетчера-Ривса. Тогда, если 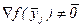для всех 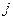, то справедливы следующие утверждения:

1) направления 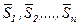являются 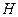- сопряжёнными;

2) направления 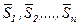являются направлениями спуска;

3) 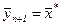- решение задачи (12.18).

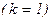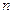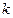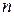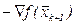Из теоремы 3.6 следует что методом Флетчера-Ривса задача (5.4) решается за одну итерацию , т. е. не более чем за одномерных поисков. При оптимизации неквадратичных функций согласно алгоритму Флетчера-Ривса после реализации каждой - ой итерации ( одномерных поисков) происходит корректировка начального направления, полагается равным , т. е. направлению наискорейшего спуска. Такое периодическое обновление направления поиска, с одной стороны, позволяет уменьшить вероятность построения линейно-зависимых направлений, уменьшает нарастающую погрешность действий, но, с другой стороны, может повлечь за собой замедление сходимости.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)