АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Достаточные условия оптимальности

Читайте также:
  1. A) подписать коллективный договор на согласованных условиях с одновременным составлением протокола разногласий
  2. I Распад аустенита в изотермических условиях
  3. I. МЕСТО И ВРЕМЯ КАК ГРАНИЧНЫЕ УСЛОВИЯ
  4. I. Неблагоприятные условия для жизни бактерий создаются при
  5. I. Правила поведения в условиях вынужденного автономного существования.
  6. I. При каких условиях эта психологическая информация может стать психодиагностической?
  7. I. Психологические условия эффективности боевой подготовки.
  8. II. Условия признания гражданина инвалидом
  9. IV. Дом - Дом, окружающая среда, внешние и внутренние условия, родители
  10. IV. ТРЕБОВАНИЯ К УЧАСТНИКАМ И ИХ УСЛОВИЯ ДОПУСКА
  11. V. Финансовые условия участия в Конкурсе
  12. VI ПРИЧИНЫ, УСЛОВИЯ И ВТОРЖЕНИЕ

Теорема 2.3. Пусть 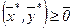– седловая точка функции Лагранжа. Тогда 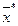– решение задачи и .

Замечание.Теоремы 2.1 и 2.3 доказаны без использования выпуклости функций 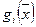, 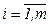и вогнутости функции 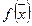, т.е. наличие седловой точки функции Лагранжа определяет оптимальность точки 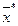для общей задачи математического программирования. Обратное утверждение, что из оптимальности точки 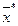следует существование седловой точки функции Лагранжа, справедливо лишь для задачи выпуклого программирования при наличии дополнительных ограничений на множестве P.

Теоремы, в которых устанавливается существование седловой точки функции Лагранжа задачи (3.4), (3.5), обычно называют теоремами Куна-Таккера.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)