III Наклонные асимптоты

Теорема. Для того, чтобы график функции имел при 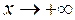наклонную асимптоту 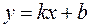, необходимо и достаточно, чтобы существовали конечные пределы

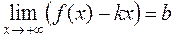и . (1)

Доказательство. Запишем уравнение прямой 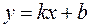в форме 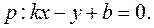Тогда можно воспользоваться готовой формулой для рас-стояния от точки графика 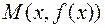до прямой :

.

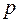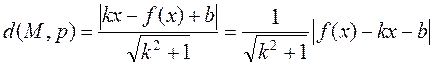Напомним ещё два результата из теории пределов:

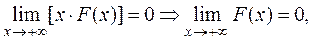ибо

Докажем необходимость. Пусть 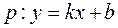– асимптота. Значит, 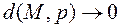при 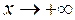, т.е. 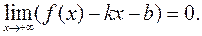Отсюда сразу имеем 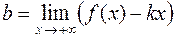. С другой стороны

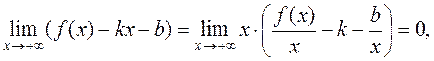
поэтому, 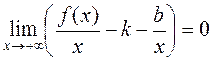, а т. к. , то и 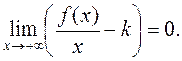Это же означает, что .

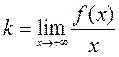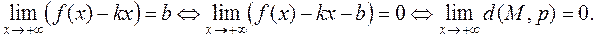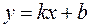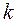Докажем достаточность. Пусть существуют пределы (1). Тогда: По определению это и означает, что прямая , где и 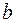определены формулами (1), является асимптотой. Теорема доказана.

Замечание 1. Аналогично определяется наклонная асимптота для случая 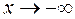. Наклонных асимптот у графика элементарной функции может быть не более двух, причём горизонтальная асимптота – это частный случай наклонной. График может пересекать свою наклонную асимптоту.

Поиск по сайту: