II Приближённые вычисления

Как уже отмечалось, остаточный член формулы Тейлора – это погрешность приближённого равенства 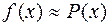, где 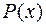– многочлен Тейлора для функции 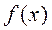. С оценкой этой погрешности 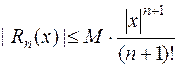(см. §3) связаны следующие задачи.

А) Какова погрешность приближённой формулы 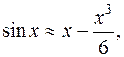если 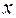изменяется в промежутке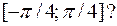

В силу пункта II, §4, для п =3 имеем

.

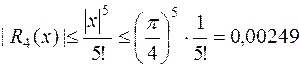Искомая погрешность не превосходит 0,0025.

В) Какой многочлен Тейлора для функции 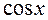обеспечит в промежутке погрешность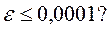

В силу пункта III, §4, имеем

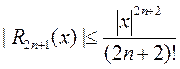
Учитывая, что 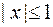, для нахождения порядка многочлена 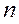, получаем неравенство 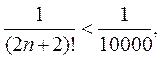т.е. .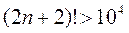

Подбором получим: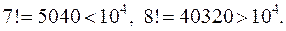

Итак, п =3 и искомый многочлен имеет вид:

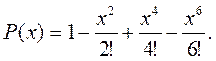
С) В каком промежутке изменения приближённая формула 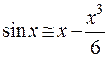обеспечит погрешность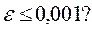

Как и в задаче А) имеем неравенство 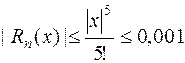или .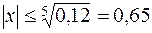

Итак, искомый промежуток изменения х – это .

Поиск по сайту: