II Точки перегиба

Определение 2. Точку называют точкой перегиба графика функции , если она отделяет участки графика с противоположными направлениями выпуклости.

Одно полезное свойство точки перегиба: если в точке перегиба существует касательная к графику функции, то она пересекает график.

Замечание 2. Часто это свойство принимают за определение точки перегиба. Но такое определение вовсе не равносильно данному выше. Кривая может и не иметь касательной в точке перегиба, а может случиться обратное: кривая пересекает касательную в точке, которая не отделяет участки с противоположными направлениями выпуклости. Примерами могут служить

функци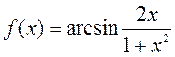и и : у первой в точках перегиба и нет касательных (хотя есть односторонние касательные), для графика второй прямые и являются касательными.

Можно привести и более интересный пример:

График этой функции в начале координат касается оси и пересекает её; здесь существует непрерывная вторая производная, но она бесконечное множество раз меняет знак в окрестности нуля. (Предоставляем читателю самому провести все необходимые вычисления для этих функций).

Приведём без доказательств ряд теорем, в которых используется понятие критической точки второго порядка.

Определение 3. Точка 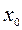называется критической точкой второго порядка функции , если вторая производная функции в этой точке равна нулю или не существует.

Теорема 2 (необходимое условие точки перегиба). Если – точка перегиба функции , то 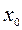– критическая точка второго порядка.

Теорема 3 (первое достаточное условие точки перегиба). Пусть 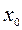– критическая точка второго порядка непрерывной функции и пусть существует такое, что в окрестностях и вторая производная существует и имеет противоположные знаки. Тогда точка – точка перегиба графика функции .

Теорема 4. (второе достаточное условие точки перегиба). Если функция имеет в точке 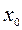конечную производную третьего порядка и удовлетворяет условиям , , 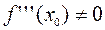то график этой функции имеет перегиб в точке .

Пример 2. Найти интервалы выпуклости и точки перегиба функции .

Решение. В предыдущем параграфе мы уже исследовали эту функцию на экстремум и получили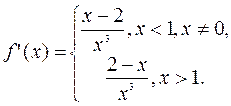

Находим вторую производную:

Напомним, что не существует в точке , значит, и не существует в этой точке, т.е. эта точка – критическая точка второго порядка. Ещё одну такую точку найдём, решив уравнение Эти критические точки разбивают область определения на интервалы знакопостоянства второй производной, т.е. интервалы выпуклости самой функции. Знаки определяем так же, как и знаки при исследовании на экстремум. Приходим к чертежу:

Итак, имеем: на интервалах 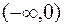, и функция выпукла вниз, а на – выпукла вверх; точки и – точки перегиба.

Замечание 3. В случае недифференцируемой функции принято другое определение выпуклости, а именно: функция называется выпуклой вниз (вверх) на интервале , если все точки любой дуги её графика лежат под (над) соответствующей хордой или на ней. Для дифференцируемой функции это определение равносильно данному выше.

Замечание 4. Третье достаточное условие перегиба будет дано в следующей теме.

Поиск по сайту: