АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Общая схема исследования функции

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. Data Mining и Business Intelligence. Многомерные представления Data Mining. Data Mining: общая классификация. Функциональные возможности Data Mining.
  3. F. Метод, основанный на использовании свойства монотонности показательной функции .
  4. I Психологические принципы, задачи и функции социальной работы
  5. I. 1.2. Общая постановка задачи линейного программирования
  6. I. Деньги и их функции.
  7. I. Личность как предмет психологического исследования
  8. I. Область исследования
  9. I. ОБЛАСТЬ ИССЛЕДОВАНИЯ
  10. I. Общая установка сознания
  11. I. Общая характеристика механизма
  12. I. Общая характеристика механизма

 

На практике для построения графика функции иногда поступают так: из уравнения находят ряд точек графика и соединяют эти точки плавной кривой. Однако, при таком методе легко пропустить какие-то важные особенности графика и допустить ошибку в построении.

Для построения графика функции необходимо исследовать её свойства. Можно предложить следующую схему исследования функции , заданной явно.

1. Найти область определения, область непрерывности, точки разрыва, пре-делы в точках разрыва и в граничных точках .

2. Найти асимптоты графика функции.

3. Вычислить производные 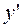и 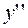и найти критические точки первого и второго порядка.

4. Составить таблицу изменения знака 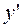и 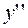(к критическим точкам следует добавить точки разрыва и граничные точки ).

5. По знакам 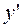найти интервалы монотонности и точки экстремума. По знакам 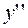найти интервалы выпуклости и точки перегиба.

6. Схематически изобразить в таблице поведение графика.

7. Нарисовать эскиз графика.

Замечания. а) Полезно исследовать функцию на четность и перио-дичность. Чётную и нечетную функции достаточно исследовать лишь для , а периодическую – на любом промежутке, длина которого равна периоду.

б) Полезно находить точки пересечения графика с осями координат.

в) Для уточнения поведения графика можно находить касательные в таких точках, как точки пересечения с осями координат, точки перегиба; в угловых точках находить односторонние касательные.

Пример. Исследовать функцию и построить график.

Решение. 1. , функция всюду непрерывная, как элемен-тарная.

2. Вертикальных асимптот нет, так как нет точек разрыва. В примере 8 предыдущего параграфа было установлено, что горизонтальных асимптот нет, а прямая является наклонной асимптотой при 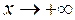и .

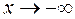3. Вычисляем производные:

 

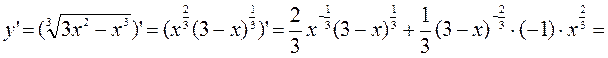
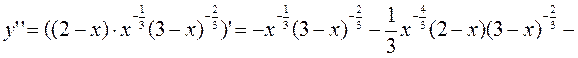
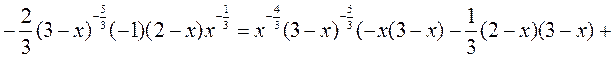
Критические точки первого порядка: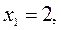

Критические точки второго порядка:

4. Составляем таблицу изменения знака производных 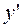и 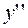. Первая строка изображает с отмеченными критическими точками. Во второй и третьей строках отмечены знаки производных в интервалах, на которые критические точки разбивают . Четвёртая строка содержит графическое изображение поведения графика функции.

 

     
– +   – –
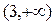
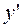
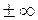
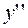
– не сущ. – – – не сущ. +
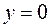
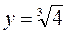
т. min т. max т. пере-гиба

 

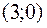
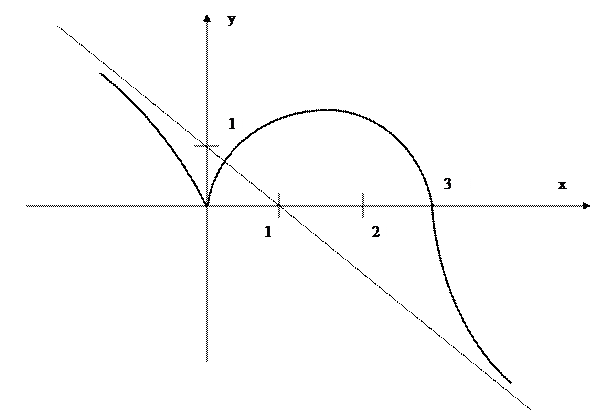
График функции изображён на рисунке

 

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)