АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств

Читайте также:
  1. FSBFRUL (Ф. Правило распределения ассигнований по КЭКР.Заголовки)
  2. III Формула Тейлора с остаточным членом в форме Лагранжа
  3. M_EOFORM (Б. Правило формирования ХО)
  4. M_EOPROV (Б. Правило формирования ХО. Проводка ХО)
  5. V2: Спектр атома водорода. Правило отбора
  6. А. Ознака успадковується «за вертикаллю», у хворої дитини, як правило, хворий один із батьків.
  7. Алгоритм метода покоординатного спуска, не использующий одномерной оптимизации.
  8. Алгоритм метода сопряжённых направлений Пауэлла для оптимизации квадратичных функций.
  9. Але монетарне правило не враховує мінливості швидкості обігу грошей та чутливості попиту до зміни процентної ставки.
  10. Бюджетное правило
  11. В/ правило Копа; г/ правило Бергмана.
  12. Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития.

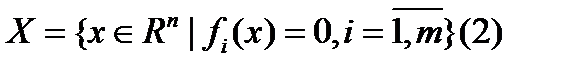
Ф-ей Лагранжа в з.(1), (2) наз. ф-ия

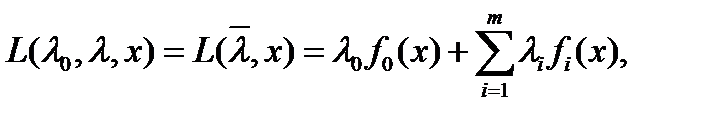
Вектор 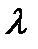наз. в-ом множ-лей Лагранжа, -обобщенным в-ом мн-лей Лагранжа.

Т-ма1(обобщ.правило мн.Л.) Пусть точка явл реш-м з.(1),(2), и пусть ф-ции непр-но диф. В окрестности т. ,тогда сущ. Такие числа что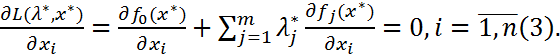

Д-во. Т.к. в рав-ах (3) 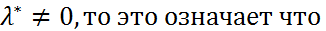- ЛЗ.Предпол-м прот-ое. Пусть система векторов (4) ЛНЗ.Тогда их кол-во не превосходит размерности пространства, т.е. . Если , то систему в-ов(4) дополним нек-ми векторами так обр., чтобы получ.с-ма в-ов (5)оставалась ЛНЗ. Построим ф-ии, зав-щие от переменных x и t: 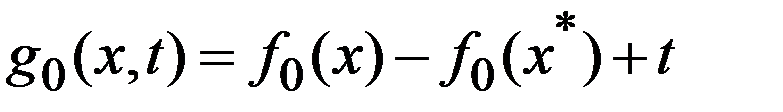, ; .Рассм.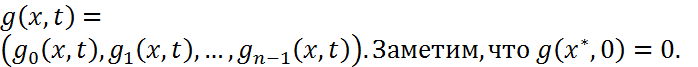

Тогда по т-ме о неявныхдля ф-циях найд. ,для которой вып.усл.1) Т.е. ф-ия удовлетворяет ограничениям з-чи и при т.е. нашли такую ф-ю удовл-щую огран-ям з-чи в кот., знач. цел.ф-ии строго<чем тому,что -явл. реш-м з.(1),(2). Зам1. Поиск точек мин-ма начинается с реш-я с-мы уравн-й относительно -переменной величины, состоящей из урав-й(3) и урав-й из (2).

Если есть решение с-мы(3), то явл. реш-м ур.(3). Т.е.множ-ли Лагранжа удовл-щие соотнош.(3) опред-ся с точностью до постоянного множителя, поэтому при реш-ии с-мы необ-х условий согласно обобщ-му правилу множ-лей Лагранжа дост-но рассм-ть случаи


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

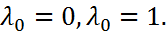
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)