 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нахождение базиса угловой точки. Пример
Рассм след вспомог задачу: Введем в рассм искусств перемен 
, ()=y≥0. (1) Т.к. мн-во 
: 
(2). И рассм задачу: 
.
Если Г1(z*)<0?,то исх задача имеет несовместную с-му ограничений. Далее будем считать Г1(z*)=0
1 случай: В симплекс-табл в мн-ве базисных пер-нных отсутсв.искуственные, то полученную таблицу можно исп. в кач-ве исходной для применения симплек-метода в реш первонач зад.. 2 случай: В с-т в соответ точке z* присутствуют искуственные переменные в списке базисных, но при этом все коэф, стоящие в строке, соответ этой искуств перем-ой и столбцам, соотв основным, перем =0, то соответс-ющие огра-ия явл линейной комбинацией ур-ний из с-мы Ах=в и это огр-ия следует удалить. Если в с-т реш зад (2,3)искуственные переменные присутствуют в мн-ве базисных и при этом в строке соответ. Этой искуственной переменной найдется положительный элемент, стоящий в столбцах соотв основ небаз пер-ным, то выбрав этот элемент в кач-ве разреш, следует перещитать с-т с целью перехода к другому базису, рассматрив угл точки.
В оставшихся сл в мн-ве осн. Перем, по опред правилам выделяем переменные, значение которых для выполнения задачи могут быть только =0
Пример 1. 
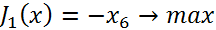
Угловая точка мн-ва планов вспомогательной задачи легко определяется. Это точка x=(0; 0; 0; 80; 0; 4), она имеет единичный базис.
| -1 | |||||||||
| Сб | Xб | СЧ | 
| 
| 
| 
| 
| 
| |
|
| 14/3 | ||||||||
| -1 |
| -1 | 4/7-> | ||||||
| -5 | -7
| -2 |
| -1 | ||||||||
| Сб | Xб | СЧ |
|
|
|
|
|
|
|
| 500/7 | 23/7 | 96/7 | 15/7 | -15/7 | |||
|
| 4/7 | 5/7 | 2/7 | -1/7 | 1/7 | |||
|
; 
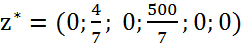Базис точки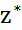 
не содержит искусственной переменной поэтому совпадает с базисом угловой точки 
мн-ва X.
Для завершения решения задачи, во второй таблице удаляем ∆-оценки, заменяем коэффициент целевой функции на коэффициент целевой функции исходной задачи. Если не предполагается дополн. анализ задачи, то столбцы искуссст. перем. можно удалить.
| -3 | -2 | -6 | |||||
| Сб | Xб | СЧ | 
| 
| 
| 
| 
|
|
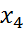
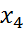
| 500/7 | 23/7 | 96/7 | 15/7 | |||
|
| 4/7 | 5/7 | 2/7 | -1/7 | |||
| J=-8/7 | 11/7 | 38/7 | 2/7 |
; 
; Минимум целевой ф-ции достигается в точке x=(0; 4/7; 0) мин знач равно 8/7.
12. Постановка ТЗ. Построение нач. плана перевозок методом северо-западного угла, методом мин. элемента.
Пусть имеется m пунктов пр-ва однородной продукции с объемами пр-ва аi, i=1,m, и n пункт.потребления этой продукции с потребностями bj, j=1,n и ∑i=1mai=∑j=1nbj.
Известны стоимости cij перевозки одной еденицы продукции из i -го пункта производства в j -ый пункт потребления. Требуется определить объем перевозок xij≥0 чтобы ∑i=1m∑j=1nсijxij→min при усл, что ∑j=1nxij=ai и ∑i=1mxij=bj
ТЗ решается с использованием таблицы спец вида, кот. наз трансп таблицей. Строки соотв пунктам производ, столбцы- пунктам потребления.В правом нижнем углу каждой клетки записыв стоим перев ед прод из i-ого в j-ый.В левй верхний угол запис перевозки, если эти перевозки не нулевые. Сумма перевозки по строкам должны = объему производства, а сумма перевозок по столбцам = объему потребления.
Положим x11=min{a1,b1}. Если a1>b1, то излишек a1-b1 завозим из А1 в пункт В2, т. е. полагаем x12=min{a1-b1,b2}. Если a1<b1, то остаток b1-a1 завозим из пункта А2, т. е. полагаем x21=min{b1-a1,а2}. Продолжая действовать по той же схеме, постепенно исчерпаем запасы в пунктах А1, …, Аn и удовлетворим запасы в пунктах В1, …, Вm т. е. получим допустимый план перевозок. Т. к. заполнение таблицы начинается с клетки {1,1} (с северо-западного угла), то метод получил название «Северо-западного угла».
Метод минимального эл-та отличается только способом выбора клетки для заполнения очередной перевозки: на каждом шаге выбирается клетка с минимальной стоимостью перевозки.
Поиск по сайту: